
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
【答案】(1)y=-![]() (0≤x≤3);(2)抛物线水柱的最大高度为
(0≤x≤3);(2)抛物线水柱的最大高度为![]() m.
m.
【解析】
试题分析:(1)以水管和地面交点为原点,原点与水柱落地点所在直线为x轴适当的直角坐标系,利用顶点式y=a(x-1)2+k,求解析式
(2)利用顶点式y=-![]() (x-1)2+
(x-1)2+![]() (0≤x≤3),知顶点坐标(1,
(0≤x≤3),知顶点坐标(1,![]() ),从而求出水柱的最大高度是
),从而求出水柱的最大高度是![]() 米。
米。
试题解析:(1)如图,以水管与地面交点为原点,原点与水柱落地点所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系.
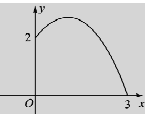
由题意可设抛物线的函数解析式为y=a(x-1)2+h(0≤x≤3)
抛物线过点(0,2)和(3,0),代入抛物线解析式得:
![]()
解得: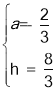
所以,抛物线的解析式为:y=-![]() (x-1)2+
(x-1)2+![]() (0≤x≤3),
(0≤x≤3),
化为一般形式为:y=-![]() (0≤x≤3)
(0≤x≤3)
(2)由(1)知抛物线的解析式为y=-![]() (x-1)2+
(x-1)2+![]() (0≤x≤3),
(0≤x≤3),
当x=1时,y=![]() ,
,
所以,抛物线水柱的最大高度为![]() m.
m.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E是边AD上一点,且AE=AB.
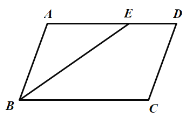
(1)作∠BCD的角平分线CF,交AD于F点,交BE于G点;(尺规作图,保留痕迹,不写画法)
(2)在(1)的条件下,
①求∠BGC的度数;
②设AB=a,BC=b,则线段EF= (用含a,b的式子表示);
③若AB=10,CF=12,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点B、C在x轴的正半轴上,反个比例函数y= ![]() (k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,
(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n, ![]() ),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
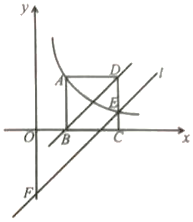
A. (0,- ![]() )B. (0,-
)B. (0,- ![]() )
)
C. (0,-3)D. (0,- ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
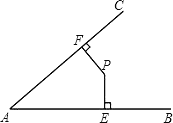
【题目】如图所示,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:
(1)PE=PF;
(2)点P在∠BAC的平分线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们规定:点![]() 关于“
关于“![]() 的衍生点”,
的衍生点”,![]() ,其中
,其中![]() 为常数且
为常数且![]() ,如:点
,如:点![]() (
(![]() ,
,![]() )关于“
)关于“![]() 的衍生点”,即
的衍生点”,即![]() ,即
,即![]() .
.
(1)求点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() 的坐标;
的坐标;
(2)若点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() ,点
,点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() ,且线段
,且线段![]() 的长度不超过线段
的长度不超过线段![]() 长度的一半,请问:是否存在
长度的一半,请问:是否存在![]() 值使得
值使得![]() 到
到![]() 轴的距离是
轴的距离是![]() 到
到![]() 轴距离的
轴距离的![]() 倍?若存在,请求出
倍?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在13×7的网格中,每个小正方形边长都是1,其顶点叫做格点,如图A、B、D、E、M、P均为格点.
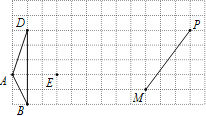
(1)请在网格中画□ABCD,要求C点在格点上.
(2)在(1)中□ABCD右侧画格点△EFG,并使EF=5,FG=3,EG=![]() .
.
(3)以MP为对角线画矩形MNPQ(M、N、P、Q按逆时针方向排列),使矩形MNPQ的面积为10.
(4)在直线AE上有一点W,使WB+WM的值最小,则这个最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边长为a,点O是对角线AC的中点,点E是BC边上的一个动点,OE⊥OF交AB边于点F,点G,H分别是点E,F关于直线AC的对称点,点E从点C运动到点B时,则图中阴影部分的面积是___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com