
【题目】如图,在Rt△BAC中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
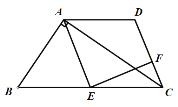
(1)求证:DC=EC.
(2)若AB=6,BC=10,求EF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据AD∥BC,AE∥DC,得到四边形AECD是平行四边形;再根据∠BAC=90°,E是BC的中点,得到AE=CE=![]() ,进而得到四边形AECD是菱形,即可证明.
,进而得到四边形AECD是菱形,即可证明.
(2)过A点作AH⊥BC于点H,根据勾股定理得到![]() ,再根据
,再根据![]() ,得到AH=
,得到AH=![]() ,再根据点E是BC的中点,BC=10,四边形AECD是菱形,得到CD=CE=5,最后根据
,再根据点E是BC的中点,BC=10,四边形AECD是菱形,得到CD=CE=5,最后根据![]() 即可求解.
即可求解.
证明:(1)∵AD∥BC,AE∥DC
∴四边形AECD是平行四边形
∵∠BAC=90°,E是BC的中点,
∴AE=CE=![]()
∴四边形AECD是菱形
∴DC=EC.
(2)过A点作AH⊥BC于点H
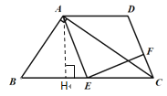
∵∠BAC=![]() ,AB=6,BC=10
,AB=6,BC=10
∴![]()
∵![]()
∴AH=![]()
∵点E是BC的中点,BC=10,四边形AECD是菱形
∴CD=CE=5
∵![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与2辆小货车一次可以运货21吨,2辆大货车与4辆小货车一次可以运货22吨.
(1)每辆大货车和每辆小货车一次各可以运货多少吨?
(2)现有这两种货车共10辆,要求一次运货不低于35吨,则其中大货车至少多少辆?(用不等式解答)
(3)日前有23吨货物需要运输,欲租用这两种货车运送,要求全部货物一次运完且每辆车必须装满.已知每辆大货车一次运货租金为300元,每辆小货车一次运货租金为200元,请列出所有的运输方案井求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点 经过点A(﹣1,0),B(5,﹣6),C(6,0)
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠AOB=90°,点C、D分别在射线OA、OB上,点E在∠AOB内部.
(1)根据语句画图形:
①画直线CE;
②画射线OE;
③画线段DE,
(2)结合图形,完成下面的填空:
①与∠ODE互补的角是 ;
②若∠BOE =![]() ∠AOE,则∠BOE的大小是 .
∠AOE,则∠BOE的大小是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,点D、E分别是边AB、AC上的两点(点D不与点A、 点B重合),且DE∥BC,以DE为一边,在四边形DBCE的内部作正方形DEFG,已知AB=AC=5,BC=6.
(1)试求△ABC的面积;
(2)当GF与BC重合时,求正方形DEFG的边长;
(3)若BG的长度等于正方形DEFG的边长,试求AD的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E是边AD上一点,且AE=AB.
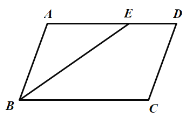
(1)作∠BCD的角平分线CF,交AD于F点,交BE于G点;(尺规作图,保留痕迹,不写画法)
(2)在(1)的条件下,
①求∠BGC的度数;
②设AB=a,BC=b,则线段EF= (用含a,b的式子表示);
③若AB=10,CF=12,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并用相关的思想方法解决问题.
计算:(1﹣![]() ﹣
﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() +
+![]() ).
).
令![]() +
+![]() +
+![]() =t,则原式=(1﹣t)(t+
=t,则原式=(1﹣t)(t+![]() )﹣(1﹣t﹣
)﹣(1﹣t﹣![]() )t=t+
)t=t+![]() ﹣t2﹣
﹣t2﹣![]() t﹣
t﹣![]() t+t2=
t+t2=![]() ,
,
问题:
(1)计算:(1﹣![]() ﹣
﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() +
+![]() );
);
(2)解方程(x2+5x+1)(x2+5x+7)=7.
查看答案和解析>>
科目:初中数学 来源: 题型:
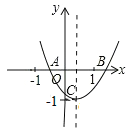
【题目】已知:二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①![]() =-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.
=-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com