
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线,分别交AD,AC于P,Q两点;(要求:尺规作图,保留作图痕迹,不写作法)
(2)证明AP=AQ.

【答案】(1)作图见解析;(2)证明见解析.
【解析】分析:(1)根据角平分线的性质作出BQ即可;
(2)先根据垂直的定义得出∠ADB=90°,故∠BPD+∠PBD=90°.再根据余角的定义得出∠AQP+∠ABQ=90°,根据角平分线的性质得出∠ABQ=∠PBD,再由∠BPD=∠APQ可知∠APQ=∠AQP,据此可得出结论.
详解:(1)如图所示,BQ为所求作

(2)∵BQ平分∠ABC ∴∠ABQ=∠CBQ
在△ABQ中,∠BAC=90°
∴∠AQP+∠ABQ=90°
∵AD⊥BC ∴∠ADB=90°
∴在Rt△BDP中,∠CBQ+∠BPD=90°
∵∠ABQ=∠CBQ ∴∠AQP=∠BPD
又∵∠BPD=∠APQ
∴∠AQP=∠AQP ∴AP=AQ


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场第1次用39万元购进A、B两种商品,销售完后获得利润6万元,它们的进价和售价如下表:(总利润=单件利润×销售量)

(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原价销售,而B商品打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于54000元,则B种商品是打几折销售的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大于1的正整数的三次方都可以分解为若干个连续奇数的和.如23=3+5,33=7+9+11,43=13+15+17+19.按此规律,若m3分解后,最后一个奇数为109,则m的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() .
.

(1)试说明![]() 成立的理由.(完成下面的填空)
成立的理由.(完成下面的填空)
证明:![]() ,
,
![]() ,(________________)
,(________________)
又![]() ,(已知)
,(已知)
![]() ,(________________)
,(________________)
![]() .(________________)
.(________________)
(2)若![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
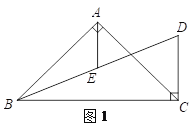
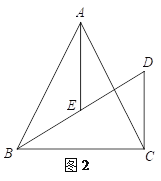
【题目】在△ABC中,AB=AC,CD⊥BC于点C,交∠ABC的平分线于点D,AE平分∠BAC交BD于点E,过点E作EF∥BC交AC于点F,连接DF.
(1)补全图1;
(2)如图1,当∠BAC=90°时,
①求证:BE=DE;
②写出判断DF与AB的位置关系的思路(不用写出证明过程);
(3)如图2,当∠BAC=α时,直接写出α,DF,AE的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
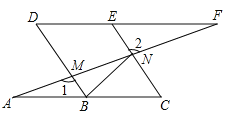
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】育才中学开展了“孝敬父母,从家务事做起”活动,活动后期随机调查了八年级部分学生一周在家做家务的时间,并将结果绘制成如下两幅尚不完整的统计图

请你根据统计图提供的信息回答下列问题:
(1)本次调查的学生总数为 人,被调查学生做家务时间的中位数是 小时,众数是 小时;
(2)请你补全条形统计图;
(3)若全校八年级共有学生1500人,估计八年级一周做家务的时间为4小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂签了1200件商品订单,要求不超过15天完成.现有甲、乙两个车间来完成加工任务。已知甲车间的加工能力是乙车间加工能力的1.5倍,并且加工240件需要的时间甲车间比乙车间少用2天.
(1)求甲、乙每个车间的加工能力每天各是多少件?
(2)甲、乙两个车间共同生产了若干天后,甲车间接到新任务,留下乙车间单独完成剩余工作,求甲、乙两车间至少合作多少天,才能保证完成任务.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com