Question

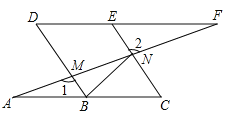
【题目】如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠A=∠F，∠1=∠2．

（1）求证：四边形BCED是平行四边形；

（2）已知DE=2，连接BN，若BN平分∠DBC，求CN的长．

Answer 1

【答案】（1）证明见解析；（2）2．

【解析】试题分析：（1）由已知角相等，利用对顶角相等，等量代换得到同位角相等，进而得出DB与EC平行，再由内错角相等两直线平行得到DE与BC平行，即可得证；

（2）由角平分线得到一对角相等，再由两直线平行内错角相等，等量代换得到一对角相等，再利用等角对等边得到CN=BC，再由平行四边形对边相等即可确定出所求．

（1）证明：∵∠A=∠F，

∴DE∥BC，

∵∠1=∠2，且∠1=∠DMF，

∴∠DMF=∠2，

∴DB∥EC，

则四边形BCED为平行四边形；

（2）解：∵BN平分∠DBC，

∴∠DBN=∠CBN，

∵EC∥DB，

∴∠CNB=∠DBN，

∴∠CNB=∠CBN，

∴CN=BC=DE=2．