【题目】原售价为m元的商品，降价30%后的价格应为( )
A. (1＋30%)m元 B. (m＋30%)元 C. (1－30%)m元 D. 30%m元
新课标快乐提优暑假作业陕西旅游出版社系列答案科目：初中数学 来源： 题型：
【题目】阅读下列材料：点A,B在数轴上分别表示有理数
。A，B两点之间的距离表示为
.当A,B两点中有一点在原点时，不妨设点A在原点，如图1所示， 
；当A,B两点都不在原点时，分三种情况，情况一：如图2所示，点A,B都在原点的右侧， 
；情况二：如图3所示，点A,B都在原点左侧， 
；情况三：如图4所示，点A,B在原点的两边， 
；综上，数轴上A,B之间的距离
.
回答下列问题：（1）数轴上表示2和5的两点之间的距离是________，数轴上表示-2和-5的两点之间的距离是____________，数轴上表示3和-1的两点之间的距离是________.
(2)数轴上表示
和-1的两点A,B之间的距离是________，如果
=2，那么
为_______.
(3)当
取最小值时， 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题探究：
1．新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”，其“面线”被该平面图形截得的线段叫做该平面图形的“面径”（例如圆的直径就是圆的“面径”）．
2．解决问题
已知等边三角形ABC的边长为2．
（1）如图一，若AD⊥BC，垂足为D，试说明AD是△ABC的一条面径，并求AD的长；
（2）如图二，若ME∥BC，且ME是△ABC的一条面径，求面径ME的长；
（3）如图三，已知D为BC的中点，连接AD，M为AB上的一点（0＜AM＜1），E是DC上的一点，连接ME，ME与AD交于点O，且S△MOA=S△DOE．
①求证：ME是△ABC的面径；
②连接AE，求证：MD∥AE；
（4）请你猜测等边三角形ABC的面径长l的取值范围（直接写出结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
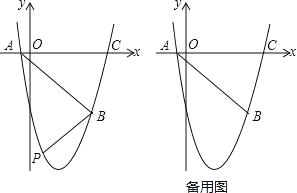
【题目】如图，抛物线y=ax2+bx+c（a、b、c为常数，a≠0）经过点A（﹣1，0），B（5，﹣6），C（6，0）．
（1）求抛物线的解析式；
（2）如图，在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）若点Q为抛物线的对称轴上的一个动点，试指出△QAB为等腰三角形的点Q一共有几个？并请求出其中某一个点Q的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平行四边形ABCD的两条对角线相交于O，且AC平分∠DAB．
（1）求证：四边形ABCD是菱形；
（2）若AC=8，BD=6，试求点O到AB的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
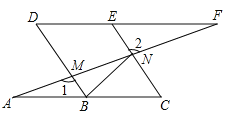
【题目】如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠A=∠F，∠1=∠2．
（1）求证：四边形BCED是平行四边形；
（2）已知DE=2，连接BN，若BN平分∠DBC，求CN的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
