
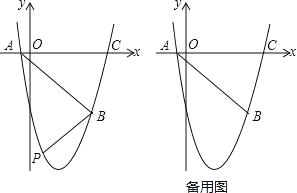
【题目】如图,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.
【答案】(1)y=x2﹣5x﹣6;(2)存在,P(2,﹣12);(3)Q点一共有5个,(![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)抛物线经过点A(﹣1,0),B(5,﹣6),C(6,0),可利用两点式法设抛物线的解析式为y=a(x+1)(x﹣6),代入B(5,﹣6)即可求得函数的解析式;(2)作辅助线,将四边形PACB分成三个图形,两个三角形和一个梯形,设P(m,m2﹣5m﹣6),四边形PACB的面积为S,用字母m表示出四边形PACB的面积S,发现是一个二次函数,利用顶点坐标求极值,从而求出点P的坐标.(3)分三种情况画图:①以A为圆心,AB为半径画弧,交对称轴于Q1和Q4,有两个符合条件的Q1和Q4;②以B为圆心,以BA为半径画弧,也有两个符合条件的Q2和Q5;③作AB的垂直平分线交对称轴于一点Q3,有一个符合条件的Q3;最后利用等腰三角形的腰相等,利用勾股定理列方程求出Q3坐标.
试题解析:(1)设y=a(x+1)(x﹣6)(a≠0),
把B(5,﹣6)代入:a(5+1)(5﹣6)=﹣6,
a=1,
∴y=(x+1)(x﹣6)=x2﹣5x﹣6;
(2)存在,
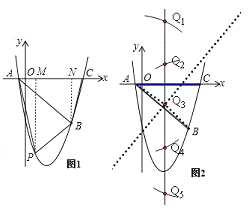
如图1,分别过P、B向x轴作垂线PM和BN,垂足分别为M、N,
设P(m,m2﹣5m﹣6),四边形PACB的面积为S,
则PM=﹣m2+5m+6,AM=m+1,MN=5﹣m,CN=6﹣5=1,BN=5,
∴S=S△AMP+S梯形PMNB+S△BNC
=![]() (﹣m2+5m+6)(m+1)+
(﹣m2+5m+6)(m+1)+![]() (6﹣m2+5m+6)(5﹣m)+
(6﹣m2+5m+6)(5﹣m)+![]() ×1×6
×1×6
=﹣3m2+12m+36
=﹣3(m﹣2)2+48,
当m=2时,S有最大值为48,这时m2﹣5m﹣6=22﹣5×2﹣6=﹣12,
∴P(2,﹣12),
(3)这样的Q点一共有5个,连接Q3A、Q3B,
y=x2﹣5x﹣6=(x﹣![]() )2﹣
)2﹣![]() ;
;
因为Q3在对称轴上,所以设Q3(![]() ,y),
,y),
∵△Q3AB是等腰三角形,且Q3A=Q3B,
由勾股定理得:(![]() +1)2+y2=(
+1)2+y2=(![]() ﹣5)2+(y+6)2,
﹣5)2+(y+6)2,
y=﹣![]() ,
,
∴Q3(![]() ,﹣
,﹣![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】素有“江南水乡”之美称的芜湖,水资源非常丰富,仅浅层地下水蕴藏量就达560 000 000 m3,数字560 000 000用科学记数法表示为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
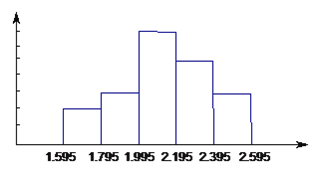
【题目】某校七年级学生进行体育测试,七年级(2)班男生的立定跳远成绩制成频数分布直方图,图中从左到右各矩形的高之比是![]() ,最后一组的频数是6,根据直方图所表达的信息,解答下列问题。
,最后一组的频数是6,根据直方图所表达的信息,解答下列问题。
(1)该班有多少名男生?
(2)若立定跳远的成绩在2.0米以上(包括2.0米)为合格率是多少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】原售价为m元的商品,降价30%后的价格应为( )
A. (1+30%)m元 B. (m+30%)元 C. (1-30%)m元 D. 30%m元
查看答案和解析>>
科目:初中数学 来源: 题型:
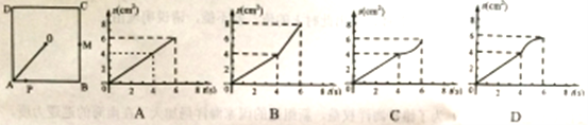
【题目】如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A—B—M方向匀速运动,到M时停止运动,速度为1cm/s. 设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图像可以是( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=﹣![]() x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=
x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=![]() MP,MB=
MP,MB=![]() OM,OE=
OM,OE=![]() ON,ND=
ON,ND=![]() NP.
NP.
(1)b= ;
(2)求证:四边形BCDE是平行四边形;
(3)在直线y=﹣![]() x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.
x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 的图象与正比例函数
的图象与正比例函数![]() 的图象交于点A(m,4).
的图象交于点A(m,4).
(1)求m、n的值;
(2)设一次函数![]() 的图象与x轴交于点B,求△AOB的面积;
的图象与x轴交于点B,求△AOB的面积;
(3)直接写出使函数![]() 的值小于函数
的值小于函数![]() 的值的自变量x的取值范围.
的值的自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线 ![]() 与x轴、y轴相交于P、Q两点,与y=
与x轴、y轴相交于P、Q两点,与y=![]() 的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB. 给出下列结论: ①k1k2<0;②m+
的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB. 给出下列结论: ①k1k2<0;②m+![]() n=0; ③S△AOP= S△BOQ;④不等式k1x+b>
n=0; ③S△AOP= S△BOQ;④不等式k1x+b>![]() 的解集是x<-2或0<x<1,其中正确的结论的序号是 .
的解集是x<-2或0<x<1,其中正确的结论的序号是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com