
【题目】如图,已知一次函数y=﹣![]() x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=
x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=![]() MP,MB=
MP,MB=![]() OM,OE=
OM,OE=![]() ON,ND=
ON,ND=![]() NP.
NP.
(1)b= ;
(2)求证:四边形BCDE是平行四边形;
(3)在直线y=﹣![]() x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.
x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.

【答案】(1)3;(2)证明见解析;(3)在直线y=﹣![]() x+b上存在这样的点P,使四边形BCDE为正方形,P点坐标是(2,2)或(﹣6,6).
x+b上存在这样的点P,使四边形BCDE为正方形,P点坐标是(2,2)或(﹣6,6).
【解析】分析:(1)根据待定系数法,可得b的值;(2)根据矩形的判定与性质,可得PM与ON,PN与OM的关系,根据PC=![]() MP,MB=
MP,MB=![]() OM,OE=
OM,OE=![]() ON,NO=
ON,NO=![]() NP,可得PC与OE,CM与NE,BM与ND,OB与PD的关系,根据全等三角形的判定与性质,可得BE与CD,BC与DE的关系,根据平行四边形的判定,可得答案;(3)根据正方形的判定与性质,可得BE与BC的关系,∠CBM与∠EBO的关系,根据全等三角形的判定与性质,可得OE与BM的关系,可得P点坐标间的关系,可得答案.
NP,可得PC与OE,CM与NE,BM与ND,OB与PD的关系,根据全等三角形的判定与性质,可得BE与CD,BC与DE的关系,根据平行四边形的判定,可得答案;(3)根据正方形的判定与性质,可得BE与BC的关系,∠CBM与∠EBO的关系,根据全等三角形的判定与性质,可得OE与BM的关系,可得P点坐标间的关系,可得答案.
本题解析:
(1)一次函数y=﹣![]() x+b的图象过点A(0,3),
x+b的图象过点A(0,3),
3=﹣![]() ×0+b,解得b=3.
×0+b,解得b=3.
故答案为:3;
(2)证明:过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,
∴∠M=∠N=∠O=90°,
∴四边形PMON是矩形,
∴PM=ON,OM=PN,∠M=∠O=∠N=∠P=90°.
∵PC=![]() MP,MB=
MP,MB=![]() OM,OE=
OM,OE=![]() ON,NO=
ON,NO=![]() NP,
NP,
∴PC=OE,CM=NE,ND=BM,PD=OB,
在△OBE和△PDC中,
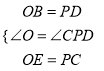 ,
,
∴△OBE≌△PDC(SAS),
BE=DC.
在△MBC和△NDE中,
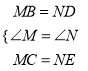 ,
,
∴△MBC≌△NDE(SAS),
DE=BC.
∵BE=DC,DE=BC,
∴四边形BCDE是平行四边形;
(3)设P点坐标(x,y),
当△OBE≌△MCB时,四边形BCDE为正方形,
OE=BM,
当点P在第一象限时,即![]() y=
y=![]() x,x=y.
x,x=y.
P点在直线上,
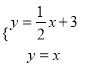 ,
,
解得![]() ,
,
当点P在第二象限时,﹣x=y
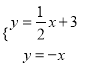 ,
,
解得![]()
在直线y=﹣![]() x+b上存在这样的点P,使四边形BCDE为正方形,P点坐标是(2,2)或(﹣6,6).
x+b上存在这样的点P,使四边形BCDE为正方形,P点坐标是(2,2)或(﹣6,6).


科目:初中数学 来源: 题型:
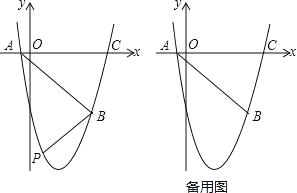
【题目】如图,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的两条对角线相交于O,且AC平分∠DAB.
(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,试求点O到AB的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
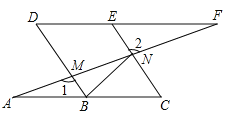
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】事件A:某人上班乘车,刚到车站车就到了;事件B:掷一枚骰子,向上一面的点数不大于6.则正确的说法是( )
A.只有事件A是随机事件
B.只有事件B是随机事件
C.都是随机事件
D.都不是随机事件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com