
【题目】如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A,B重合),点F在BC边上(不与点B,C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;依次操作下去…
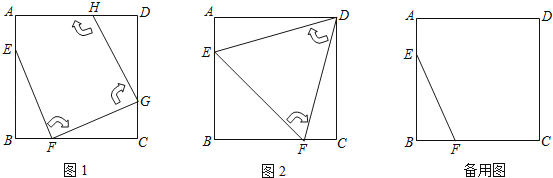
(1)图2中的△EFD是经过两次操作后得到的,其形状为 ,
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 ,此时AE与BF的数量关系是 ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围。
【答案】(1)等边三角形;(2)正方形;AE=BF; =2(x-2)2+8,8≤y<16.
【解析】
试题分析:(1)由旋转性质,易得△EFD是等边三角形;利用等边三角形的性质、勾股定理求出EF的长;
(2)①四边形EFGH的四边长都相等,所以是正方形;利用三角形全等证明AE=BF;
②求面积y的表达式,这是一个二次函数,利用二次函数性质求出最值及y的取值范围.
试题解析:(1)如题图2,由旋转性质可知EF=DF=DE,则△DEF为等边三角形.
在Rt△ADE与Rt△CDF中,
![]()
∴Rt△ADE≌Rt△CDF(HL)
∴AE=CF.
设AE=CF=x,则BE=BF=4-x
∴△BEF为等腰直角三角形.
∴EF=![]() BF=
BF=![]() (4-x).
(4-x).
∴DE=DF=EF=![]() (4-x).
(4-x).
在Rt△ADE中,由勾股定理得:AE2+AD2=DE2,即:x+42=[![]() (4-x]2,
(4-x]2,
解得:x1=8-4![]() ,x2=8+4
,x2=8+4![]() (舍去)
(舍去)
∴EF=![]() (4-x)=4
(4-x)=4![]() -4
-4![]() .
.
DEF的形状为等边三角形,EF的长为4![]() -4
-4![]() .
.
(2)①四边形EFGH的形状为正方形,此时AE=BF.理由如下:
依题意画出图形,如答图1所示:
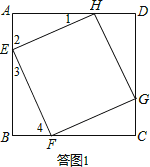
由旋转性质可知,EF=FG=GH=HE,∴四边形EFGH的形状为正方形.
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
∵∠3+∠4=90°,∠2+∠3=90°,
∴∠2=∠4.
在△AEH与△BFE中,
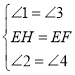
∴△AEH≌△BFE(ASA)
∴AE=BF.
②利用①中结论,易证△AEH、△BFE、△CGF、△DHG均为全等三角形,
∴BF=CG=DH=AE=x,AH=BE=CF=DG=4-x.
∴y=S正方形ABCD-4S△AEH=4×4-4×![]() x(4-x)=2x2-8x+16.
x(4-x)=2x2-8x+16.
∴y=2x2-8x+16(0<x<4)
∵y=2x2-8x+16=2(x-2)2+8,
∴当x=2时,y取得最小值8;当x=0时,y=16,
∴y的取值范围为:8≤y<16.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )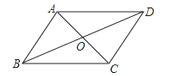
A.AB∥DC,AD=BC
B.AB∥DC,AD∥BC
C.AB=DC,AD=BC
D.OA=OC,OB=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随州市尚市“桃花节”观赏人数逐年增加,据有关部门统计,2014年约为20万人次,2016年约为28.8万人次,设观赏人数年均增长率为x,则下列方程中正确的是( )
A.20(1+2x)=28.8
B.28.8(1+x)2=20
C.20(1+x)2=28.8
D.20+20(1+x)+20(1+x)2=28.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC, ![]() BAC=40°,将△ABC绕点A按逆时针方向旋转100°得到△ADE,连接BD,CE交于点F.
BAC=40°,将△ABC绕点A按逆时针方向旋转100°得到△ADE,连接BD,CE交于点F.
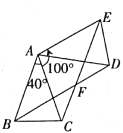
(1)求证:△ABD≌△ACE;
(2)求证:四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是一块等边三角形场地,点D,E分别是AC,BC边上靠近C点的三等分点.现有一个机器人(点P)从A点出发沿AB边运动,观察员选择了一个固定的位置记录机器人的运动情况.设AP=x,观察员与机器人之间的距离为y,若表示y与x的函数关系的图象大致如图2所示,则观察员所处的位置可能是图1的( )

A. 点B B. 点C C. 点D D. 点E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(0,4),点M是线段AB上任意一点(A,B两点除外)。
(1)求直线AB的解析式;
(2)过点M分别作MC⊥OA于点C,MD⊥OB于点D,当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(3)当点M把线段AB分成的两部分的比为1:3时,请求出点M的坐标。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com