
 已知,如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠1=60°,AE=2.
已知,如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠1=60°,AE=2.分析 (1)根据AD∥BC,∠1与∠2是内错角,因而就可以求得∠2,根据图形的折叠的定义,可以得到∠4=∠2,进而可以求得∠3的度数;
(2)已知AE=2,在Rt△ABE中,根据三角函数就可以求出AB、BE的长,BE=DE,则可以求出AD的长,就可以得到矩形的面积.
解答 解:(1)∵AD∥BC,
∴∠2=∠1=60°;
又∵∠4=∠2=60°,
∴∠3=180°-60°-60°=60°.
(2)在直角△ABE中,由(1)知∠3=60°,
∴∠5=90°-60°=30°;
∴BE=2AE=4,
∴AB=2$\sqrt{3}$;
∴AD=AE+DE=AE+BE=2+4=6,
∴长方形纸片ABCD的面积S为:AB•AD=2$\sqrt{3}$×6=12$\sqrt{3}$.
点评 此题考查了矩形的性质,折叠的性质以及直角三角形的性质.注意数形结合思想以及建模思想的运用是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 2014年全国两会民生活题再次成为社会焦点,央视记者为了了解百姓“两会民生话题”的聚焦点,随机调查了部分北京市民,并对结果进行整理.绘制了如下不完整的统计图表.
2014年全国两会民生活题再次成为社会焦点,央视记者为了了解百姓“两会民生话题”的聚焦点,随机调查了部分北京市民,并对结果进行整理.绘制了如下不完整的统计图表. | 组别 | 焦点话题 | 人数 |
| A | 食品安全 | 80 |
| B | 教育医疗 | M |
| C | 就业养老 | 100 |
| D | 生态环保 | 120 |
| E | 其它 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
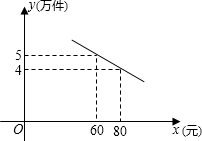 某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元,在销售过程中发现,年销售量y(万件)与销售单价x(元)之间存在着如图所示的一次函数关系.
某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元,在销售过程中发现,年销售量y(万件)与销售单价x(元)之间存在着如图所示的一次函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
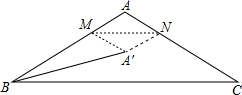 如图,在△ABC中,∠BAC=120°,AB=AC=4,点M,N分别在边AB,AC上,将△AMN沿MN翻折,点A的对应点为A′,连接BA′,则BA′长度的最小值为4$\sqrt{3}-4$.
如图,在△ABC中,∠BAC=120°,AB=AC=4,点M,N分别在边AB,AC上,将△AMN沿MN翻折,点A的对应点为A′,连接BA′,则BA′长度的最小值为4$\sqrt{3}-4$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
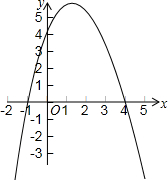 已知二次函数y=-x2+3x+4的图象.
已知二次函数y=-x2+3x+4的图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com