
如图15,从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC.
(1)求这个扇形的面积;
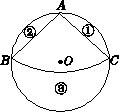
(2)在剩下的材料中,能否从③中剪出一个圆作为底面,与扇形ABC围成一个圆锥?若不能,请说明理由;若能,请求出剪的圆的半径是多少.
解:(1)如答图7所示,连接BC.
由∠BAC=90°得BC为⊙O的直径,
∴BC=4.
在Rt△ABC中,由勾股定理可得:AB=AC=2 ,
,
∴S扇形ABC=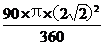 =2π.
=2π.
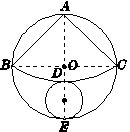
答图7
(2)不能.
如答图7所示,连接AO并延长交⌒BC于点D,交⊙O于点E,则
DE=4-2 .
.
而l⌒BC=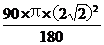 =
= π,
π,
设能与扇形ABC围成圆锥的底面圆的直径为d,
则dπ= π,
π,
∴d= .
.
又∵DE=4-2 <d=
<d= ,即围成圆锥的底面圆的直径大于DE,
,即围成圆锥的底面圆的直径大于DE,
∴不能围成圆锥.
点拨:(1)由勾股定理求出扇形的半径,再根据扇形面积公式求值.(2)题需要求出③中最大圆的直径以及圆锥底面圆的直径(圆锥底面圆的周长即为弧BC的长),然后进行比较即可.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图5①.在图5②中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图5①所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是( )
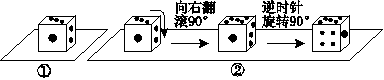
图5
A.6 B.5 C.3 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图4,已知AB是⊙O的直径,AD切⊙O于点A,点C是⌒EB的中点,则下列结论不成立的是( )
A.OC//AE B.EC=BC
C.∠DAE=∠ABE D.AC⊥OE
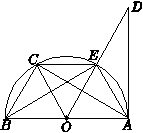
查看答案和解析>>
科目:初中数学 来源: 题型:
如图10,△ABC为等边三角形,AB=6,动点O在△ABC的边上从点A出发沿着A→C→B→A的路线匀速运动一周,速度为每秒1个单位长度,以O为圆心、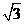 为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第________秒.
为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第________秒.
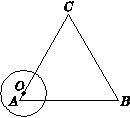
查看答案和解析>>
科目:初中数学 来源: 题型:
一纸箱内有红、黄、蓝、绿四种颜色的纸牌,且图1所示为各颜色纸牌数量的统计图.若小华自箱内抽出一张牌,且每张牌被抽出的机会相等,则他抽出红色牌或黄色牌的机(概)率为( )
A.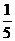 B.
B.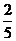 C.
C. D.
D.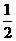

图1
查看答案和解析>>
科目:初中数学 来源: 题型:
如图6,电路图上有编号为①②③④⑤⑥共6个开关和一个小灯泡,闭合开关①或同时闭合开关②③或同时闭合开关④⑤⑥都可使这个小灯泡发光,问任意闭合电路上其中的两个开关,小灯泡发光的概率为_______.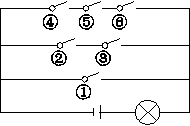
查看答案和解析>>
科目:初中数学 来源: 题型:
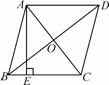
如图,已知菱形ABCD的对角线AC、BD的长分别为6 cm、8 cm,AE⊥BC于点E,则AE的长是( )
A.5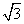 cm B.2
cm B.2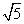 cm C.
cm C. cm D.
cm D.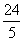 cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com