练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在离水面高度为5米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为13米，此人以0.5米每秒的速度收绳，10秒后船移动到点D的位置，问船向岸边移动了多少米？（假设绳子是直的，结果保留根号）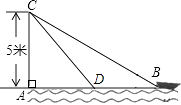

    【答案】解：在Rt△ABC中： ∵∠CAB=90°，BC=13米，AC=5米，
    ∴AB= =12（米），
    ∵此人以0.5米每秒的速度收绳，10秒后船移动到点D的位置，
    ∴CD=13﹣0.5×10=8（米），
    ∴AD= = = （米），
    ∴BD=AB﹣AD=12﹣ （米），
    答：船向岸边移动了（12﹣ ）米
    【解析】在Rt△ABC中，利用勾股定理计算出AB长，再根据题意可得CD长，然后再次利用勾股定理计算出AD长，再利用AB=AD可得BD长．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一个角的补角是这个角余角的3倍，则这个角是度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一组数据8，3，8，6，7，8，7的众数和中位数分别是（ ）
    A.8，6
    B.7，6
    C.7，8
    D.8，7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC是直角三角形，∠ACB=90°．

    （1）尺规作图：作⊙C，使它与AB相切于点D，与AC相交于点E，保留作图痕迹，不写作法，请标明字母；

    （2）在你按（1）中要求所作的图中，若BC=3，∠A=30°，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知射线CD∥OA，点E、点F是OA上的动点，CE平分∠OCF，且满足∠FCA=∠FAC．

    （1）若∠O=∠ADC，判断AD与OB的位置关系，证明你的结论．
    （2）若∠O=∠ADC=60°，求∠ACE的度数．
    （3）在（2）的条件下左右平行移动AD，∠OEC和∠CAD存在怎样的数量关系？请直接写出结果（不需写证明过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合题
    （1）如图（1），将一副直角三角板的直角顶点C叠放在一起．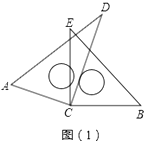

    ①填空：∠ACE∠BCD（选填“＜”或“＞”或“＝”）；
    ②若∠DCE=25°，求∠ACB的度数；
    ③猜想∠ACB与∠DCE的数量关系，并说明理由.
    （2）若改变（1）中一个三角板的位置，如图（2）所示，则上述第③题的结论是否仍然成立？（不需要说明理由）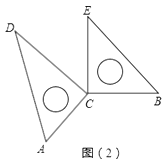

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小彬是学校的篮球队长，在一场篮球比赛中，他一人得了25分，其中罚球得了5分，他投进的2分球比3分球多5个，则他本场比赛3分球进了（　　）

    A. 1个

    B. 2个

    C. 3个

    D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：抛物线经过点A（2，﹣3）和B（4，5）．

    （1）求抛物线的表达式及顶点坐标；

    （2）将抛物线沿x轴翻折，得到图象G1，求图象G1的表达式；

    （3）设B点关于对称轴的对称点为E，抛物线G2：（a≠0）与线段EB恰有一个公共点，结合函数图象，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线EF，CD相交于点0，OA⊥OB，且OC平分∠AOF，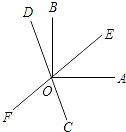

    （1）若∠AOE=40°，求∠BOD的度数；
    （2）若∠AOE=α，求∠BOD的度数；（用含α的代数式表示）
    （3）从（1）（2）的结果中能看出∠AOE和∠BOD有何关系？

    查看答案和解析>>

    同步练习册答案