
【题目】已知:抛物线![]() 经过点A(2,﹣3)和B(4,5).
经过点A(2,﹣3)和B(4,5).
(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图象G1,求图象G1的表达式;
(3)设B点关于对称轴的对称点为E,抛物线G2:![]() (a≠0)与线段EB恰有一个公共点,结合函数图象,求a的取值范围.
(a≠0)与线段EB恰有一个公共点,结合函数图象,求a的取值范围.

【答案】(1)![]() ,顶点坐标为(1,﹣4);(2)
,顶点坐标为(1,﹣4);(2)![]() ;(3)
;(3)![]() ≤a<
≤a<![]() .
.
【解析】
试题分析:(1)根据待定系数法求得即可;
(2)根据关于x轴对称的点的坐标特征即可求得;
(3)由于BE∥x轴,把B、E两点坐标代入![]() 可计算出对应的a的值,然后根据抛物线C2:
可计算出对应的a的值,然后根据抛物线C2:![]() (a≠0)与线段BE恰有一个公共点可确定a的范围.
(a≠0)与线段BE恰有一个公共点可确定a的范围.
试题解析:(1)把A(2,﹣3)和B(4,5)分别代入![]()
得:![]() ,解得:
,解得:![]() ,∴抛物线的表达式为:
,∴抛物线的表达式为:![]() .
.
∵![]() =
=![]() ,∴顶点坐标为(1,﹣4);
,∴顶点坐标为(1,﹣4);
(2)∵将抛物线沿x轴翻折,得到图象G1与原抛物线图形关于x轴对称,∴图象G1的表达式为:![]() ;
;
(3)∵B(4,5),对称轴:x=1,∴B点关于对称轴的对称点E点坐标为(﹣2,5),当G2过E点时,代入E(﹣2,5),则a=![]() ,当G2过B点时,代入B(4,5),则a=
,当G2过B点时,代入B(4,5),则a=![]() ,所以a的取值范围为
,所以a的取值范围为![]() ≤a<
≤a<![]() .
.


 互动课堂系列答案
互动课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P,则∠APN的度数为( ) 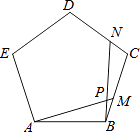
A.120°
B.118°
C.110°
D.108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号) 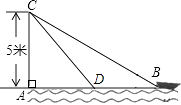
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( ) 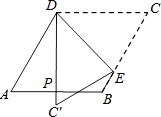
A.78°
B.75°
C.60°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
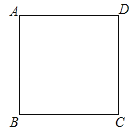
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】
用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
【问题探究】
不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以先从特殊入手,通过试验、观察、类比、最后归纳、猜测得出结论.
【探究一】
(1)用3根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
此时,显然能搭成一种等腰三角形.
所以,当n=3时,m=1.
(2)用4根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形.
所以,当n=4时,m=0.
(3)用5根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形.
所以,当n=5时,m=1.
(4)用6根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形.
所以,当n=6时,m=1.
综上所述,可得:表①

【探究二】
(1)用7根相同的木棒搭一个三角形,能搭成多少种不同的三角形?
(仿照上述探究方法,写出解答过程,并将结果填在表②中)
(2)用8根、9根、10根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
表②

你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
【问题解决】:
用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(设n分别等于4k﹣1,4k,4k+1,4k+2,其中k是正整数,把结果填在表③中)
表③

【问题应用】:
用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(写出解答过程),其中面积最大的等腰三角形每腰用了 根木棒.(只填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
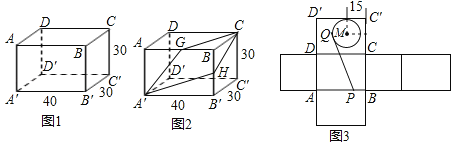
【题目】图1、图2为同一长方体房间的示意图,图3为该长方体的表面展开图.
(1)蜘蛛在顶点A′处.
①苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线;
②苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近;
(2)在图3中,半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,蜘蛛P在线段AB上,苍蝇Q在⊙M的圆周上,线段PQ为蜘蛛爬行路线,若PQ与⊙M相切,试求PQ长度的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com