
【题目】已知⊙O的直径AB=2,弦AC与弦BD交于点E.且OD⊥AC,垂足为点F.

(1)如图1,如果AC=BD,求弦AC的长;
(2)如图2,如果E为弦BD的中点,求∠ABD的余切值;
(3)联结BC、CD、DA,如果BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,求△ACD的面积.
【答案】(1)AC=![]() ;(2)cot∠ABD=
;(2)cot∠ABD=![]() ;(3)S△ACD=
;(3)S△ACD=![]() .
.
【解析】(1)由AC=BD知![]() ,得
,得![]() ,根据OD⊥AC知
,根据OD⊥AC知![]() ,从而得
,从而得![]() ,即可知∠AOD=∠DOC=∠BOC=60°,利用AF=AOsin∠AOF可得答案;
,即可知∠AOD=∠DOC=∠BOC=60°,利用AF=AOsin∠AOF可得答案;
(2)连接BC,设OF=t,证OF为△ABC中位线及△DEF≌△BEC得BC=DF=2t,由DF=1﹣t可得t=![]() ,即可知BC=DF=
,即可知BC=DF=![]() ,继而求得EF=
,继而求得EF=![]() AC=
AC=![]() ,由余切函数定义可得答案;
,由余切函数定义可得答案;
(3)先求出BC、CD、AD所对圆心角度数,从而求得BC=AD=![]() 、OF=
、OF=![]() ,从而根据三角形面积公式计算可得.
,从而根据三角形面积公式计算可得.
(1)∵OD⊥AC,
∴![]() ,∠AFO=90°,
,∠AFO=90°,
又∵AC=BD,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴∠AOD=∠DOC=∠BOC=60°,
∵AB=2,
∴AO=BO=1,
∴AF=AOsin∠AOF=1×![]() =
=![]() ,
,
则AC=2AF=![]() ;
;
(2)如图1,连接BC,
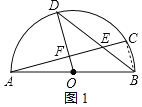
∵AB为直径,OD⊥AC,
∴∠AFO=∠C=90°,
∴OD∥BC,
∴∠D=∠EBC,
∵DE=BE、∠DEF=∠BEC,
∴△DEF≌△BEC(ASA),
∴BC=DF、EC=EF,
又∵AO=OB,
∴OF是△ABC的中位线,
设OF=t,则BC=DF=2t,
∵DF=DO﹣OF=1﹣t,
∴1﹣t=2t,
解得:t=![]() ,
,
则DF=BC=![]() 、AC=
、AC=![]() =
=![]() ,
,
∴EF=![]() FC=
FC=![]() AC=
AC=![]() ,
,
∵OB=OD,
∴∠ABD=∠D,
则cot∠ABD=cot∠D=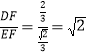 ;
;
(3)如图2,
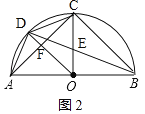
∵BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,
∴∠BOC=![]() 、∠AOD=∠COD=
、∠AOD=∠COD=![]() ,
,
则![]() +2×
+2×![]() =180,
=180,
解得:n=4,
∴∠BOC=90°、∠AOD=∠COD=45°,
∴BC=AC=![]() ,
,
∵∠AFO=90°,
∴OF=AOcos∠AOF=![]() ,
,
则DF=OD﹣OF=1﹣![]() ,
,
∴S△ACD=![]() ACDF=
ACDF=![]() ×
×![]() ×(1﹣
×(1﹣![]() )=
)=![]() .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】数学是神秘奇妙的,数与字母有着密切的联系,字母可以表示数,数可以赋予字母其值,以下是某同学参加校庆举办的“越战越勇”活动的一道思考题,请同学们帮他完成,
(1)填表:
|
| |
用代数式表示 |
| |
|
| |
| ||
|
根据表中计算结果,你发现了什么等式?请写出这个等式
(2)利用(1)中发现的结论,计算![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +8 |
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
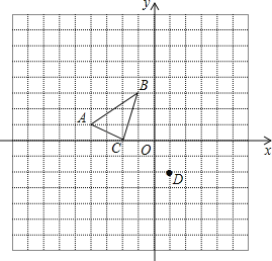
【题目】如图,三角形ABC三个顶点的坐标分别是A(-4,1),B(-1,3),C(-2,0),将三角形ABC平移得到三角形DEF,使点A与点D(1,-2)是对应点.
(1)在图中画出三角形DEF,并写出点B、C的对应点E、F的坐标;
(2)若点P在x轴上,且知三角形PCD的面积等于三角形ABC面积的![]() ,请写出满足条件的点P的坐标.
,请写出满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“一带一路”国际合作高峰论坛在北京举行,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区.已知甲种商品的销售单价为900元,乙种商品的销售单价为600元.
(1)已知乙种商品的销售量不能低于甲种商品销售量的三分之一,则最多能销售甲种商品多少万件?
(2)在(1)的条件下,要使甲、乙两种商品的销售总收入不低于5700万元,请求甲种商品销售量的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,∠CDE=25°,现将△CDE沿直线DE翻折得到△FDE,连接BF,则∠BFE的度数是_____.
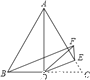
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:(1)△BDA≌△AEC;(2)DE=BD+CE.
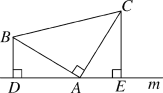
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com