
【题目】如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,∠CDE=25°,现将△CDE沿直线DE翻折得到△FDE,连接BF,则∠BFE的度数是_____.
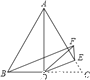
【答案】85°
【解析】
根据等边三角形的性质可得∠C=60°,根据等腰三角形三线合一的性质可得BD=CD,根据翻折变换的性质可得CD=DF,∠DFE=∠C,∠CDE=∠FDE,从而得到BD=DF,根据等边对等角可得∠DBF=∠DFB,然后根据三角形的一个外角等于与它不相邻的两个内角的和可得∠CDF=∠DBF+∠DFB,从而求出∠DFB,再根据∠BFE=∠DFB+∠DFE计算即可得解.
解:∵△ABC是等边三角形,
∴∠C=60°,
∵AD是BC边上的中线,
∴BD=CD,
∵△CDE沿直线DE翻折得到△FDE,
∴CD=DF,∠DFE=∠C=60°,∠CDE=∠FDE=25°,
∴BD=DF,
∴∠DBF=∠DFB,
由三角形的外角性质得,∠CDF=∠DBF+∠DFB=2∠DFB,
∴∠DFB=![]() ∠CDF=∠CDE=25°,
∠CDF=∠CDE=25°,
∴∠BFE=∠DFB+∠DFE=25°+60°=85°.


科目:初中数学 来源: 题型:
【题目】观察下面三行数
![]() ①
①
![]() ②
②
![]() ③
③
![]() 第①行的第
第①行的第![]() 个数可表示为 ;
个数可表示为 ;
![]() 第②③行数与第①行数分别有什么关系?
第②③行数与第①行数分别有什么关系?
![]() 取每行的第
取每行的第![]() 个数,从上到下依次把这三个数记为
个数,从上到下依次把这三个数记为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的直径AB=2,弦AC与弦BD交于点E.且OD⊥AC,垂足为点F.

(1)如图1,如果AC=BD,求弦AC的长;
(2)如图2,如果E为弦BD的中点,求∠ABD的余切值;
(3)联结BC、CD、DA,如果BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
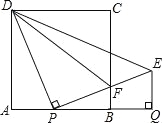
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准备组织七年级160名学生参加社会实践活动,租用35座和45座两种客车共四辆,每种客车至少租1辆,可以坐不满.
(1)参加本次活动至少需几辆45座客车?
(2)如果35座客车的租金为每辆300元,45座客车的租金为每辆400元,要想使全部租车的费用不超过1550元,则有几种租车的方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).请根据图中提供的信息解答下列问题:
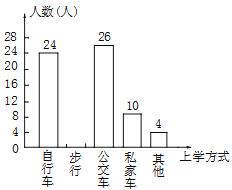
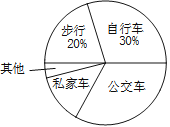
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)在扇形统计图中,“公交车”部分所对应的圆心角是多少度?
(4)若全校有1600名学生,估计该校乘坐私家车上学的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥BC,垂足为C,AC=2cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_____秒时,△BCA与点P、N、B为顶点的三角形全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠A=∠D,说明∠F与∠C相等的理由.
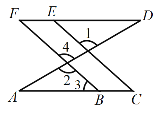
解:∵∠1=∠2( 已知 ),∠2=∠4 ( ),
∴∠1=∠4( 等量代换 ),
∴FB∥EC( ),
∴∠3=∠C( 两直线平行,同位角相等 ).
∵∠A=∠D( ),
∴ED∥AC( ),
∴∠F=∠3 ( ),
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com