
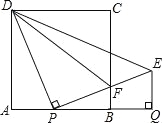
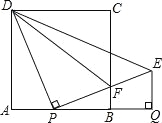
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.
【答案】(1)1(2)点P是AB的中点
【解析】
试题分析:(1)由题意得:PD=PE,∠DPE=90°,又由正方形ABCD的边长为1,易证得△ADP≌△QPE,然后由全等三角形的性质,求得线段PQ的长;
(2)易证得△DAP∽△PBF,又由△PFD∽△BFP,根据相似三角形的对应边成比例,可得证得PA=PB,则可求得答案.
试题解析:(1)根据题意得:PD=PE,∠DPE=90°,
∴∠APD+∠QPE=90°,
∵四边形ABCD是正方形,
∴∠A=90°,
∴∠ADP+∠APD=90°,
∴∠ADP=∠QPE,
∵EQ⊥AB,
∴∠A=∠Q=90°,
在△ADP和△QPE中,
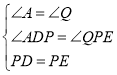 ,
,
∴△ADP≌△QPE(AAS),
∴PQ=AD=1;
(2)∵△PFD∽△BFP,
∴![]() ,
,
∵∠ADP=∠EPB,∠CBP=∠A,
∴△DAP∽△PBF,
∴![]() ,
,
∴![]() ,
,
∴PA=PB,
∴PA=![]() AB=
AB=![]()
∴当PA=![]() ,即点P是AB的中点时,△PFD∽△BFP.
,即点P是AB的中点时,△PFD∽△BFP.


科目:初中数学 来源: 题型:
【题目】某商店以每件120元的价格卖出两件衣服,其中一件盈利20%,另一件亏损20%,则卖出这两件衣服商家总的盈亏情况是_____(盈利或亏损多少元).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x﹣2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.
(1)求a,k的值;
(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标;
(3)在抛物线及其对称轴上分别取点M、N,使以A,C,M,N为顶点的四边形为正方形,求此正方形的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“2008北京”奥运会国家体育场的“鸟巢“钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为4.6×108帕的钢材,那么4.6×108帕的原数为( ).
A.4 600 000
B.46 000 000
C.460 000 000
D.4 600 000 000
查看答案和解析>>
科目:初中数学 来源: 题型:
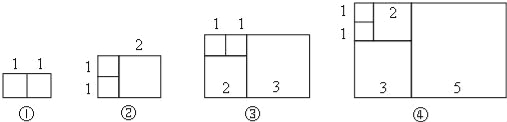
【题目】如图,将边长分别为1、2、3、5、…的若干正方形按一定的规律拼成不同的矩形,依次记作矩形①、矩形②、矩形③、矩形④,那么按此规律.
(1)组成第n个矩形的正方形的个数为 个;
(2)求矩形⑥的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种病菌的直径为0.00000471cm,把数据0.00000471用科学记数法表示为( )
A. 47.1×10﹣4B. 4.71×10﹣5C. 4.71×10﹣7D. 4.71×10﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
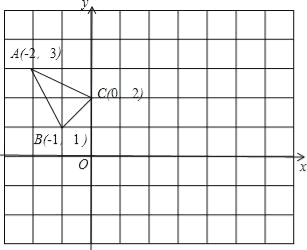
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.
(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com