
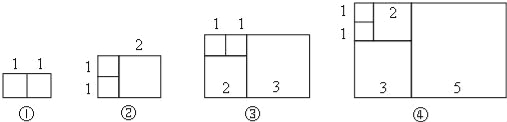
【题目】如图,将边长分别为1、2、3、5、…的若干正方形按一定的规律拼成不同的矩形,依次记作矩形①、矩形②、矩形③、矩形④,那么按此规律.
(1)组成第n个矩形的正方形的个数为 个;
(2)求矩形⑥的周长.
【答案】(1)(n+1)个(2)68
【解析】
试题分析:(1)由矩形①、②、③中正方形个数即可得知;结合图形分析,①的周长为:2(1+2),②的周长为:2(2+3),③的周长为:2(3+5),④的周长为:2(5+8),由此可推出第n个长方形的宽为第n﹣1个长方形的长,第n个长方形的长为第n﹣1个长方形的长和宽的和,据此可得.
试题解析:(1)∵矩形①中,正方形个数为1;矩形②中,正方形个数为3;矩形③中,正方形个数为4;…,
∴组成第n个矩形的正方形的个数为(n+1)个;
(2)∵①的周长为:2(1+2),
②的周长为:2(2+3),
③的周长为:2(3+5),
④的周长为:2(5+8),
由此可推出第n个长方形的宽为第n﹣1个长方形的长,
第n个长方形的长为第n﹣1个长方形的长和宽的和.
可得:第⑤个的周长为:2(8+13),
第⑥的周长为:2(13+21)=68;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知ABCD的周长为8 cm,∠B=30°,若边长AB为x cm.
(1)写出ABCD的面积y(cm2)与x(cm)的函数关系式,并求自变量x的取值范围.
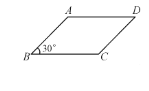
(2)当x取什么值时,y的值最大?并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
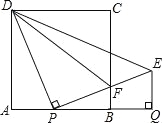
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
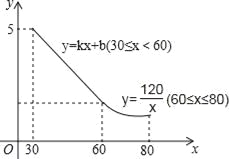
【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年某区域GDP(区域内生产总值)总量为90.03亿元,用科学计数法表示90.03亿为( )
A. 9.003×1010B. 9.003×109C. 9.003×108D. 90.03×108
查看答案和解析>>
科目:初中数学 来源: 题型:
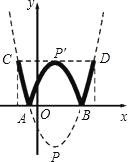
【题目】已知:如图,抛物线y=a(x﹣1)2+c与x轴交于点A(![]() ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级5班的小明在解答此题时顿生灵感:过点P′作x轴的平行线交抛物线于C、D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比![]() (约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:
(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:![]() ,
,![]() ,结果可保留根号)
,结果可保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com