
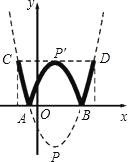
【题目】已知:如图,抛物线y=a(x﹣1)2+c与x轴交于点A(![]() ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级5班的小明在解答此题时顿生灵感:过点P′作x轴的平行线交抛物线于C、D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比![]() (约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:
(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:![]() ,
,![]() ,结果可保留根号)
,结果可保留根号)
【答案】(1)y=x2﹣2x﹣2(2)0.6124
【解析】
试题分析:(1)利用P与P′(1,3)关于x轴对称,得出P点坐标,利用待定系数法求出二次函数的解析式即可;
(2)根据已知得出C,D两点坐标,进而得出“W”图案的高与宽(CD)的比.
试题解析:(1)∵P与P′(1,3)关于x轴对称,
∴P点坐标为(1,﹣3);
∵抛物线y=a(x﹣1)2+c过点A(![]() ,0),顶点是P(1,﹣3),
,0),顶点是P(1,﹣3),
∴ ;
;
解得![]() ;
;
则抛物线的解析式为y=(x﹣1)2﹣3,…
即y=x2﹣2x﹣2.
(2)∵CD平行x轴,P′(1,3)在CD上,
∴C、D两点纵坐标为3;
由(x﹣1)2﹣3=3,
解得:![]() ,
,![]()
∴C、D两点的坐标分别为(![]() ,3),(
,3),(![]() ,3)
,3)
∴CD=![]()
∴“W”图案的高与宽(CD)的比=![]() (或约等于0.6124).
(或约等于0.6124).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
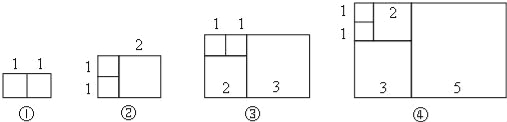
【题目】如图,将边长分别为1、2、3、5、…的若干正方形按一定的规律拼成不同的矩形,依次记作矩形①、矩形②、矩形③、矩形④,那么按此规律.
(1)组成第n个矩形的正方形的个数为 个;
(2)求矩形⑥的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
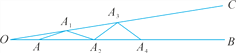
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按以下要求画图:以点A为圆心,1为半径向右画弧交OC于点A1,得第一条线段AA1;再以点A1为圆心,1为半径向右画弧交OB于点A2,得第二条线段A1A2;再以点A2为圆心,1为半径向右画弧交OC于点A3,得第三条线段A2A3……这样一直画下去,最多能画____条线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明:“若整数系数一元二次方程ax2+bx+c=0(a≠0)有有理根,则a,b,c中至少有一个是偶数”,下列假设中正确的是( )
A. 假设a,b,c都是偶数 B. 假设a,b,c都不是偶数
C. 假设a,b,c至多有一个是偶数 D. 假设a,b,c至多有两个是偶数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)12﹣(﹣18)+(﹣7)﹣15
(2)(﹣ ![]() )×
)× ![]() ÷(﹣
÷(﹣ ![]() )
)
(3)( ![]() +
+ ![]() ﹣
﹣ ![]() )×(﹣12)
)×(﹣12)
(4)﹣10+8÷(﹣2)2﹣(﹣4)×(﹣3)
(5)﹣22×0.125﹣[4÷(﹣ ![]() )2﹣
)2﹣ ![]() ]+(﹣1)2013 .
]+(﹣1)2013 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com