
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+2x+c��x�ύ��A����1��0��B��3��0�����㣬��y�ύ�ڵ�C����D�Ǹ������ߵĶ��㣮
��1���������ߵĽ���ʽ��ֱ��AC�Ľ���ʽ��
��2������y������һ��M��ʹ��BDM���ܳ���С�������M�����ꣻ
��3����̽�����ڒ��������Ƿ���ڵ�P��ʹ�Ե�A��P��CΪ���㣬ACΪֱ�DZߵ���������ֱ�������Σ������ڣ���������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1�������߽���ʽΪy=��x2+2x+3��ֱ��AC�Ľ���ʽΪy=3x+3����2����M������Ϊ��0��3����
��3�����������ĵ�P������Ϊ��![]() ��
��![]() ����
����![]() ����
����![]() ����
����
����������1���轻��ʽy=a��x+1����x-3����չ���õ�-2a=2��Ȼ�����a���ɵõ������߽���ʽ����ȷ��C��0��3����Ȼ�����ô���ϵ������ֱ��AC�Ľ���ʽ��
��2�����ö��κ���������ȷ��D������Ϊ��1��4������B�����y��ĶԳƵ�B��������DB����y����M����ͼ1����B�䣨-3��0������������֮���߶���̿��жϴ�ʱMB+MD��ֵ��С�����ʱ��BDM���ܳ���С��Ȼ�����ֱ��DB���Ľ���ʽ���ɵõ���M�����ꣻ
��3������C��AC�Ĵ��߽�����������һ��P����ͼ2��������ֱ�ߴ�ֱһ����ϵ����Ϊ��������ֱ��PC�Ľ���ʽΪy=-![]() x+b����C������������b�õ�ֱ��PC�Ľ���ʽΪy=-
x+b����C������������b�õ�ֱ��PC�Ľ���ʽΪy=-![]() x+3���ٽⷽ����
x+3���ٽⷽ����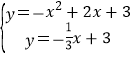 �ô�ʱP�����ꣻ������A��AC�Ĵ��߽�����������һ��Pʱ������ͬ���ķ����������ʱP�����꣮
�ô�ʱP�����ꣻ������A��AC�Ĵ��߽�����������һ��Pʱ������ͬ���ķ����������ʱP�����꣮
��1���������߽���ʽΪy=a��x+1����x��3����
��y=ax2��2ax��3a��
����2a=2�����a=��1��
�������߽���ʽΪy=��x2+2x+3��
��x=0ʱ��y=��x2+2x+3=3����C��0��3����
��ֱ��AC�Ľ���ʽΪy=px+q��
��A����1��0����C��0��3�������![]() �����
�����![]() ��
��
��ֱ��AC�Ľ���ʽΪy=3x+3��
��2����y=��x2+2x+3=����x��1��2+4��
�ඥ��D������Ϊ��1��4����
��B�����y��ĶԳƵ�B��������DB����y����M����ͼ1����B�䣨��3��0����
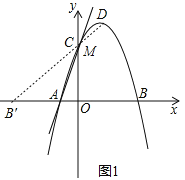
��MB=MB�䣬
��MB+MD=MB��+MD=DB������ʱMB+MD��ֵ��С��
��BD��ֵ���䣬
���ʱ��BDM���ܳ���С��
��ֱ��DB���Ľ���ʽΪy=x+3��
��x=0ʱ��y=x+3=3��
���M��������0��3����
��3�����ڣ�
����C��AC�Ĵ��߽�����������һ��P����ͼ2��
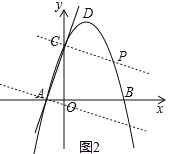
��ֱ��AC�Ľ���ʽΪy=3x+3��
��ֱ��PC�Ľ���ʽ����Ϊy=��![]() x+b��
x+b��
��C��0��3�������b=3��
��ֱ��PC�Ľ���ʽΪy=��![]() x+3��
x+3��
�ⷽ����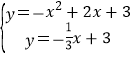 �����
�����![]() ��
��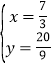 �����ʱP������Ϊ��
�����ʱP������Ϊ��![]() ��
��![]() ����
����
����A��AC�Ĵ��߽�����������һ��P��ֱ��PC�Ľ���ʽ����Ϊy=��![]() x+b��
x+b��
��A����1��0�������![]() +b=0�����b=��
+b=0�����b=��![]() ��
��
��ֱ��PC�Ľ���ʽΪy=��![]() x��
x��![]() ��
��
�ⷽ����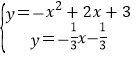 �����
�����![]() ��
��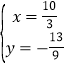 �����ʱP������Ϊ��
�����ʱP������Ϊ��![]() ����
����![]() ��.
��.
�������������������ĵ�P������Ϊ��![]() ��
��![]() ������
������![]() ����
����![]() ��.
��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
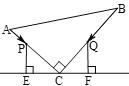
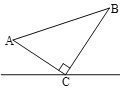
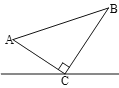
����Ŀ����ͼ��ʾ����ABC�У���ACB=90�㣬AC=6cm��BC =8cm.��P��A�����,��![]() ·�����յ�B�˶�����Q��B�����,��
·�����յ�B�˶�����Q��B�����,��![]() ·�����յ�A�˶�.��P ��Q�ֱ�
·�����յ�A�˶�.��P ��Q�ֱ�![]() ��
��![]() ���˶��ٶ�ͬʱ��ʼ�˶������㶼Ҫ����Ӧ���յ�ʱ����ֹͣ�˶�����ijʱ�̣��ֱ����P��Q��PE��l��E��QF��l��F.���P�˶�������ʱ����PEC�͡�CFQȫ�ȣ���˵������.
���˶��ٶ�ͬʱ��ʼ�˶������㶼Ҫ����Ӧ���յ�ʱ����ֹͣ�˶�����ijʱ�̣��ֱ����P��Q��PE��l��E��QF��l��F.���P�˶�������ʱ����PEC�͡�CFQȫ�ȣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB=BC=5��tan��ABC=![]() ��
��
��1�����AC�ij���
��2�����BC�Ĵ�ֱƽ�������AB�Ľ���ΪD����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
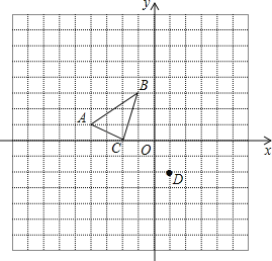
����Ŀ����ͼ��������ABC�������������ֱ���A��-4��1����B��-1��3����C��-2��0������������ABCƽ�Ƶõ�������DEF��ʹ��A���D��1��-2���Ƕ�Ӧ�㣮
��1����ͼ�л���������DEF����д����B��C�Ķ�Ӧ��E��F�����ꣻ
��2������P��x���ϣ���֪������PCD���������������ABC�����![]() ����д�����������ĵ�P�����꣮
����д�����������ĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ��һ·�����ʺ����߷���̳�ڱ������У��й�ͬ30�������ǩ��ó����Э�飬ij���������ס���������Ʒ��8���������һ��һ·�����߹��Һ͵�������֪������Ʒ�����۵���Ϊ900Ԫ��������Ʒ�����۵���Ϊ600Ԫ��
��1����֪������Ʒ�����������ܵ��ڼ�����Ʒ������������֮һ������������ۼ�����Ʒ���������
��2���ڣ�1���������£�Ҫʹ�ס���������Ʒ�����������벻����5700��Ԫ�����������Ʒ�������ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����A��ԭ����������Ḻ�����˶�,ͬʱ����BҲ��ԭ������������������˶�,2���,�������16����λ���ȣ���֪����A��B���ٶȱ�Ϊ1:3(�ٶȵ�λ:1����λ������).
![]()
(1)�����������˶����ٶȣ�
(2)�������ϱ��A��B�����ԭ������˶�2��ʱ��λ�ã�
(3)����ʾ��0�ĵ��ΪO��A��B����ֱ��(2)�б����λ��ͬʱ�����Ḻ�����˶�,�پ����ʱ��,����OB=2OA?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
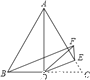
����Ŀ����ͼ����ABC�ǵȱ������Σ�AD��BC���ϵ����ߣ���E��AC�ϣ���CDE��25�����ֽ���CDE��ֱ��DE���۵õ���FDE������BF�����BFE�Ķ�����_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
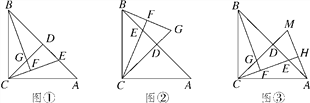
����Ŀ����ͼ�٣��ڡ�ABC�У�AC��BC����ACB��90��������C��CD��AB�ڵ�D����E��AB����һ����(�����˵�A��B)������CE������B��CE�Ĵ��߽�ֱ��CE�ڵ�F����ֱ��CD�ڵ�G.
(1)��֤��AE��CG��
(2)����E�˶����߶�BD��ʱ(��ͼ��)���Բ���AE��CG��������ϵ�Ƿ����仯����д����Ľ��ۣ�
(3)����A��AH��CE������Ϊ��H������CD���ӳ����ڵ�M(��ͼ��)���ҳ�ͼ����BE��ȵ��߶Σ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
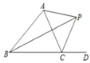
����Ŀ����ͼ ,��ABC �����ƽ���� CP ���ڽ�ƽ���� BP �ཻ�ڵ� P,����BPC=25�������CAP=__________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com