
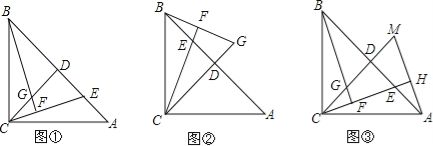
����Ŀ����ͼ�٣��ڡ�ABC�У�AC��BC����ACB��90��������C��CD��AB�ڵ�D����E��AB����һ����(�����˵�A��B)������CE������B��CE�Ĵ��߽�ֱ��CE�ڵ�F����ֱ��CD�ڵ�G.
(1)��֤��AE��CG��
(2)����E�˶����߶�BD��ʱ(��ͼ��)���Բ���AE��CG��������ϵ�Ƿ����仯����д����Ľ��ۣ�
(3)����A��AH��CE������Ϊ��H������CD���ӳ����ڵ�M(��ͼ��)���ҳ�ͼ����BE��ȵ��߶Σ���֤����
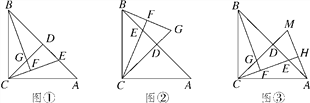
���𰸡���1������������2����������3��BE��CM.
�����������⣨1����ͼ�������ݵ���ֱ�������ε����ʿ��Եó���BCD=��ACD=45��������ֱ�������ε������ε����ʾͿ��Եó���CBF=��ACE����ASA�Ϳ��Եó���BCG�ա�CAE���Ϳ��Եó����ۣ�
��2����ͼ�������ݵ���ֱ�������ε����ʿ��Եó���BCD=��ACD=45��������ֱ�������ε������ε����ʾͿ��Եó���CBF=��ACE����ASA�Ϳ��Եó���BCG�ա�CAE���Ϳ��Եó����ۣ�
��3����ͼ�������ݵ���ֱ�������ε����ʿ��Եó���BCD=��ACD=45��������ֱ�������ε������ε����ʾͿ��Եó���BCE=��CAM����ASA�Ϳ��Եó���BCE�ա�CAM���Ϳ��Եó����ۣ�
�⣺��1����AC=BC��
���ABC=��CAB��
�ߡ�ACB=90����
���ABC=��A=45������ACE+��BCE=90����
��BF��CE��
���BFC=90����
���CBF+��BCE=90����
���ACE=��CBF
����RT��ABC��CD��AB��AC=BC��
���BCD=��ACD=45��
���A=��BCD��
����BCG����ACE��
 ��
��
���BCG�ա�ACE��ASA����
��AE=CG��
��2�����䣮AE=CG��
���ɣ���AC=BC��
���ABC=��CAB��
�ߡ�ACB=90����
���ABC=��A=45������ACE+��BCE=90����
��BF��CE��
���BFC=90����
���CBF+��BCE=90����
���ACE=��CBF
����RT��ABC��CD��AB��AC=BC��
���BCD=��ACD=45��
���A=��BCD��
����BCG����ACE��
 ��
��
���BCG�ա�ACE��ASA����
��AE=CG��
��3��BE=CM��
����AC=BC��
���ABC=��CAB��
�ߡ�ACB=90����
���ABC=��A=45������ACE+��BCE=90����
��AH��CE��
���AHC=90����
���HAC+��ACE=90����
���BCE=��HAC��
����RT��ABC��CD��AB��AC=BC��
���BCD=��ACD=45��
���ACD=��ABC��
����BCE����CAM��
 ��
��
���BCE�ա�CAM��ASA����
��BE=CM��


 ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬѧ�Ƕ�֪����|5������2��|��ʾ5�멁2֮��ľ���ֵ��ʵ����Ҳ������Ϊ5�멁2����������������Ӧ������֮��ľ��룮������������������̽����
![]()
��1�������ϱ�ʾ5�멁2����֮��ľ������� ��
��2�������ϱ�ʾx��2������֮��ľ�����Ա�ʾΪ�� ����
��3��ͬ��|x+3|+|x��1|��ʾ������������x����Ӧ�ĵ㵽��3��1����Ӧ�ĵ�ľ���֮�ͣ������ҳ����з�������������x��ʹ��|x+3|+|x��1|=4���������������� ����
��4��������̽������|x+10|+|x+2|+|x��8|�Ƿ�����Сֵ������У�ֱ��д����Сֵ�����û�У�˵�����ɣ�
��5��������̽������|x+10|+|x+2|+|x��8|+|x��10|�Ƿ�����Сֵ������У�ֱ��д����Сֵ�����û�У�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
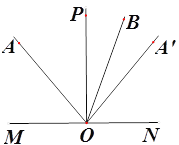
����Ŀ����ͼ��ƽ����һ����A��ֱ��MN���Ϸ�����OΪֱ��MN��һ���� ��������OA��OP��OA��������O��ֱ��MN���˶�ʱ��ʼ�ձ��֡�MOP=90�㡢��AOP=��A��OP��������OA�Ƶ�O˳ʱ����ת60��õ�����OB
��1����ͼ������O�˶���ʹ��A������OP����࣬��OBƽ�֡�A��OP�����AOP�Ķ�����
��2������O�˶���ʹ��A������OP����࣬��AOM=3��A��OBʱ����![]() ��ֵ��
��ֵ��
��3������O�˶���ijһʱ��ʱ����A��OB=150�㣬ֱ��д����BOP= ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij����װ����һ���������A��һ�������������B����������С�������һЩ���ݺ���Щ���ݾ���װ�ü�����������Ӧ����������������װ�õļ�����ɣ������������10������������ǣ�������
A | 1 | 2 | 3 | 4 | 5 |
B | 0 | 3 | 8 | 15 | 24 |
A. 99 B. 100 C. 101 D. 102
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ABΪ��O��ֱ����OC��AB����DC��OB���ڵ�F����ֱ��AB����һ��F������ED������ED=EF�� 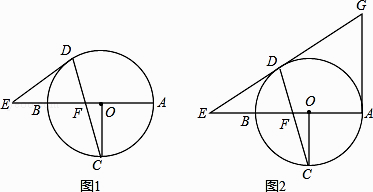
��1����ͼ1����֤��EDΪ��O�����ߣ�
��2����ͼ2��ֱ��ED������AG�ཻ��G����OF=2����O�İ뾶Ϊ6����AG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��PA������A��-1��0������P��1��2����ֱ��PB��һ�κ���y=-x+3��ͼ����
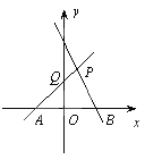
��1����ֱ��PA�ı���ʽ��Q������ꣻ
��2�����ı���PQOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��Ԫ¥�������·ݵ��õ�(��λ����)�����������õ�����������ȷ����(����)
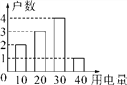
A. ����Ϊ30 B. ��λ��Ϊ30 C. ƽ����Ϊ24 D. ����Ϊ84
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵��������![]() =��1����a��b��Ϊ�෴��������a+b��0����
=��1����a��b��Ϊ�෴��������a+b��0����![]() ��0����|a+2b|=��a��2b����һ���������������������������Ϊ0��1��������1��a��0����a2����
��0����|a+2b|=��a��2b����һ���������������������������Ϊ0��1��������1��a��0����a2����![]() ������a+b+c��0��ab��0��c��0����|��a|=��a��������ȷ�ĸ����ǣ�������
������a+b+c��0��ab��0��c��0����|��a|=��a��������ȷ�ĸ����ǣ�������
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬѧÿ����ѧ����ѧʹ�ù������������������������������100Ԫ������˳�������![]() ��ʾ���������ϵ������
��ʾ���������ϵ������![]() ��ʾ��
��ʾ��
���� | ��� |
1 |
|
2 |
|
3 |
|
�� | �� |
(1)������ݱ����е���Ϣ���������4�γ˳��������ϵ���
(2)����д����ͬѧ�������ϵ����![]() ��˳�����
��˳�����![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
(3)�����ͬѧ�����20�γ�������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com