
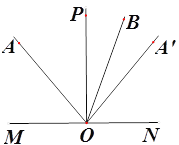
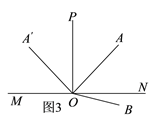
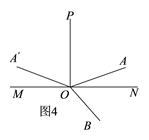
����Ŀ����ͼ��ƽ����һ����A��ֱ��MN���Ϸ�����OΪֱ��MN��һ���� ��������OA��OP��OA��������O��ֱ��MN���˶�ʱ��ʼ�ձ��֡�MOP=90�㡢��AOP=��A��OP��������OA�Ƶ�O˳ʱ����ת60��õ�����OB
��1����ͼ������O�˶���ʹ��A������OP����࣬��OBƽ�֡�A��OP�����AOP�Ķ�����
��2������O�˶���ʹ��A������OP����࣬��AOM=3��A��OBʱ����![]() ��ֵ��
��ֵ��
��3������O�˶���ijһʱ��ʱ����A��OB=150�㣬ֱ��д����BOP= ��.
���𰸡�(1) ��AOP=40�㣻(2) ![]() ��6�� (3) 105��135.
��6�� (3) 105��135.
�����������������
��1���������ã���AOB=60������AOP=��A��OP=2��POB���ɴ˿ɵá�AOP+��POB=3��POB=60�㣬������á�POB=20�㣬���ɵõ���AOP=40����
��2����������OB�ڡ�A��OP���ڲ�ʱ����ͼ1�����A��OB= ![]() ������AOM=
������AOM=![]() ����AON=
����AON=![]() ����AOA��=
����AOA��= ![]() ���ɴ˿ɵ���AOP=��A��OP=
���ɴ˿ɵ���AOP=��A��OP=![]() ������AOM+��AOP=��MOP=90���ɵ�
������AOM+��AOP=��MOP=90���ɵ�![]() �����
�����![]() ���ɴ˼�����á�AON�͡�AOP���Ӷ���������ǵı�ֵ��
���ɴ˼�����á�AON�͡�AOP���Ӷ���������ǵı�ֵ��
��������OB�ڡ�AON���ڲ�ʱ����ͼ2�����A��OB= ![]() ������AOM=
������AOM=![]() ����AON=
����AON=![]() ����AOA��=
����AOA��= ![]() ���ɴ˿ɵ���AOP=��A��OP=
���ɴ˿ɵ���AOP=��A��OP=![]() ������AOM+��AOP=��MOP=90���ɵ�
������AOM+��AOP=��MOP=90���ɵ�![]() �����
�����![]() ���ɴ˼�����á�AON�͡�AOP���Ӷ���������ǵı�ֵ��
���ɴ˼�����á�AON�͡�AOP���Ӷ���������ǵı�ֵ��
��3����ͼ3������A��OB=150��ʱ���á�A��OA=150��-60��=90���������AOP=��A��OP�ɵ���AOP=45�����Ӷ��ɵ���BOP=60��+45��=105������ͼ4������A��OB=150��ʱ���á�A��OA=360��-150��-60��=150���������AOP=��A��OP�ɵ���AOP=75�����Ӷ��ɵ���BOP=60��+75��=135����
���������
��1��������ɵã���AOB=60������AOP=��A��OP��
��OBƽ����A��OP��
����A��OP=2��POB��
����AOP=��A��OP=2��POB��
���AOB=��AOP+��POB=3��POB=60����
���POB=20����
���AOP=2��POB=40����
(2)������O�˶���ʹ��A������OP�������������OB���ڡ�A��OP���ڲ�ʱ����ͼ1��
����A��OB=x������AOM=3��A��OB=3x����AOA��= ![]() ��
��
��OP��MN��
���AON=180��-3����AOP=90��-3x��
��![]() ��
��
�ߡ�AOP=��A��OP��
���AOP=��A��OP=![]()
��![]() ����ã�
����ã� ![]() ��
��
��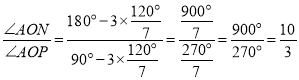 ��
��
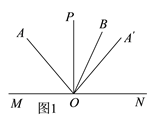
�ڵ���O�˶���ʹA������OP����࣬��������OB�ڡ�A��ON�ڲ�ʱ����ͼ2��
���A��OB=x�����AOM=3x����AON=![]() ����AOA��=
����AOA��= ![]() ��
��
�ߡ�AOP=��A��OP��
���AOP=��A��OP=![]() ��
��
��OP��MN��
���AOP=90-��AOM=90-3x��
��![]() �������
������� ![]() ��
��
��![]() ��
��
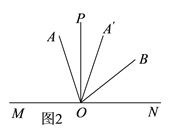
��3������ͼ3������A��OB=150��ʱ��
��ͼ�ɵã���A��OA=��A��OB-��AOB=150��-60��=90����
���ߡ�AOP=��A��OP��
����AOP=45����
����BOP=60��+45��=105����
����ͼ4������A��OB=150��ʱ����ͼ�ɵ���A��OA=360��-150��-60��=150����
���ߡ�AOP=��A��OP��
����AOP=75����
���BOP=60��+75��=135����
������������BOP�Ķ���Ϊ105���135��.


 ��ҵ����ϵ�д�
��ҵ����ϵ�д� ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ƻ�Ͷ��һ���ʽ�ɹ�һ��������Ʒ�������г����鷢�֣�����³����ۣ��ɻ���15���������ñ����������Ͷ��������Ʒ������ĩ�ֿɻ���10���������ĩ���ۿɻ���30������Ҫ�����ִ�����700Ԫ��
��1�����̳�Ͷ��![]() Ԫ���ֱ��ú�
Ԫ���ֱ��ú�![]() �Ĵ���ʽ��ʾ�³����ۺ���ĩ��������õ�����
�Ĵ���ʽ��ʾ�³����ۺ���ĩ��������õ�����
��2�����̳�Ͷ��40000Ԫ����ѡ���������۷�ʽ�����϶ࣿ��ʱ��������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��������һ���⣺����![]() �������ʽ��7a3��6a3b+3a2b+3a3+6a3b��3a2b��10a3+3��ֵ����С��ϸ����һ�£������������������
�������ʽ��7a3��6a3b+3a2b+3a3+6a3b��3a2b��10a3+3��ֵ����С��ϸ����һ�£������������������![]() �Ƕ���ģ������������һ�£���Ϊ����˵���Ƿ��е�����
�Ƕ���ģ������������һ�£���Ϊ����˵���Ƿ��е�����
��2��С������һ����ѧ�⣺����֪��������ʽΪA��B������B=4a2��5a��6����A+B��ֵ�������ĵ�С������A+B�����ɡ�A��B�����������Ĵ���10a��7a2+12���������С�������ȷ��A+B�Ľ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACΪֱ������O��BC�ڵ�D����AB�ڵ�G����D��BC���е㣬DE��AB������ΪE����AC���ӳ����ڵ�F�� 
��1����֤��ֱ��EF�ǡ�O�����ߣ�
��2��CF=5��cos��A= ![]() ����AE�ij���
����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʢʢͬѧ��ij��У����ʱ�������˶������������еIJ�����Ϣ�����±�����
Ժϵ�������ɼ����� | |||
�������� | ʤ�� | ���� | ���� |
22 | 12 | 10 | 34 |
22 | 14 | 8 | 36 |
22 | 0 | 22 | 22 |
ʢʢͬѧ���ѧϰ��֪ʶ������������⣬�����æ����������⣺
��1���ӱ��п��Կ�������һ����______��,ʤһ����_______����
��2��ij���ڱ���22����ǰ���£�ʤ���ܻ����ܵ����为���ܻ��ֵ�2������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���BAC��90����AB��AC����DΪBC���е㣬ֱ�ǡ�MDN�Ƶ�D��ת��DM��DN�ֱ����AB��AC����E��F���㣬���н��ۣ��١�DEF�ǵ���ֱ�������Σ���AE��CF���ۡ�BDE�ա�ADF����BE��CF��EF��������ȷ�������� ��

A. �٢ڢ� B. �ڢۢ�
C. �٢ڢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪[x]��ʾ������x�������������[3]=3��[3.14]=3��[��3.14]=��4��
�������Ϲ������������⣺
��1��[��8]=�� ����[5.4]=�� ����[��6.99]=�� ����
��2����[x]=��5����x�ķ�Χ���� ����
��3����֪������nС��100��![]() =n��2����������������������n��
=n��2����������������������n��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
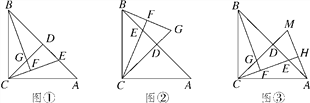
����Ŀ����ͼ�٣��ڡ�ABC�У�AC��BC����ACB��90��������C��CD��AB�ڵ�D����E��AB����һ����(�����˵�A��B)������CE������B��CE�Ĵ��߽�ֱ��CE�ڵ�F����ֱ��CD�ڵ�G.
(1)��֤��AE��CG��
(2)����E�˶����߶�BD��ʱ(��ͼ��)���Բ���AE��CG��������ϵ�Ƿ����仯����д����Ľ��ۣ�
(3)����A��AH��CE������Ϊ��H������CD���ӳ����ڵ�M(��ͼ��)���ҳ�ͼ����BE��ȵ��߶Σ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A��B���㣬�ֱ��Ӧ����Ϊa��b����֪��a+1��2��|b��3|��Ϊ�෴������PΪ������һ���㣬��ӦΪx��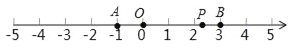
��1��a=������b=�� ��
��2������P����A�͵�B�ľ�����ȣ����P��Ӧ�������� ��
��3���������Ƿ���ڵ�P��ʹ��P����A�͵�B�ľ���֮��Ϊ5�������ڣ������x��ֵ���������ڣ�˵�����ɣ�
��4��|x��a|+|x��b|����Сֵ=�� ��
��5������P��ÿ����1����λ���ȵ��ٶȴ�O�������˶�����A��ÿ����5����λ���������˶����ʼ�����ʱ��P����A����B�ľ�����ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com