
ЎѕМвДїЎїИзНјЈєКэЦбЙПУРAЎўBБЅµгЈ¬·Ц±р¶ФУ¦µДКэОЄaЈ¬bЈ¬ТСЦЄЈЁa+1Ј©2Ул|b©Ѓ3|»ҐОЄПа·ґКэЈ®µгPОЄКэЦбЙПТ»¶ЇµгЈ¬¶ФУ¦ОЄxЈ®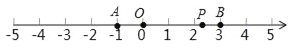
ЈЁ1Ј©a=ЎЎЎЎЈ»b=ЎЎ ЎЎ
ЈЁ2Ј©ИфµгPµЅµгAєНµгBµДѕаАлПаµИЈ¬ФтµгP¶ФУ¦µДКэКЗЎЎ ЎЎ
ЈЁ3Ј©КэЦбЙПКЗ·сґжФЪµгPЈ¬К№µгPµЅµгAєНµгBµДѕаАлЦ®єНОЄ5ЈїИфґжФЪЈ¬ЗлЗуіцxµДЦµЈ»ИфІ»ґжФЪЈ¬ЛµГчАнУЙЈ»
ЈЁ4Ј©|x©Ѓa|+|x©Ѓb|µДЧоРЎЦµ=ЎЎ ЎЎ
ЈЁ5Ј©µ±µгPТФГї·ЦЦУ1ёцµҐО»і¤¶ИµДЛЩ¶ИґУOµгПтЧуФЛ¶ЇЈ¬µгAТФГї·ЦЦУ5ёцµҐО»і¤¶ИПтЧуФЛ¶ЇЈ¬ОКјё·ЦЦУК±µгPµЅµгAЎўµгBµДѕаАлПаµИЈї
Ўѕґр°ёЎї(1) ©Ѓ1Ј¬3Ј»(2)1;(3) x1=©Ѓ1.5Ј¬x2=3.5Ј»(4)4;(5) ![]() ·ЦЦУК±µгPµЅµгAЎўµгBµДѕаАлПаµИ
·ЦЦУК±µгPµЅµгAЎўµгBµДѕаАлПаµИ
ЎѕЅвОцЎї
ЈЁ1Ј©ёщѕЭЈЁa+1Ј©2Ул|b-3|»ҐОЄПа·ґКэЈ¬їЙТФЗуµГaЎўbµДЦµЈ»
ЈЁ2Ј©ёщѕЭМвТвїЙТФµГµЅ№ШУЪxµД·ЅіМЈ¬ґУ¶шїЙТФЗуµГxµДЦµЈ»
ЈЁ3Ј©ёщѕЭМвТвїЙТФБРіц№ШУЪxµД·ЅіМЈ¬±ѕМвµГТФЅвѕцЈ»
ЈЁ4Ј©ёщѕЭМвТвЈ¬АыУГ·ЦАаМЦВЫµДЛјПлїЙТФЅвґр±ѕМвЈ»
ЈЁ5Ј©ёщѕЭМвТвїЙТФБРіцПаУ¦µД·ЅіМЈ¬±ѕМвµГТФЅвѕц.
Ѕв:ЈЁ1Ј©ЎЯЈЁa+1Ј©2Ул|b©Ѓ3|»ҐОЄПа·ґКэЈ¬
Ўаa+1=0Ј¬b©Ѓ3=0Ј¬
ЅвµГЈ¬a=©Ѓ1Ј¬b=3Ј¬
№Кґр°ёОЄЈє©Ѓ1Ј¬3Ј»
ЈЁ2Ј©УЙМвТвїЙµГЈ¬
|x©ЃЈЁ©Ѓ1Ј©|=|x©Ѓ3|Ј¬
ЅвµГЈ¬x=1Ј¬
№Кґр°ёОЄЈє1Ј»
ЈЁ3Ј©КэЦбЙПґжФЪµгPЈ¬К№µгPµЅµгAєНµгBµДѕаАлЦ®єНОЄ5Ј¬
УЙМвТвїЙµГЈ¬
|x©ЃЈЁ©Ѓ1Ј©|+|x©Ѓ3|=5Ј¬
ЅвµГЈ¬x1=©Ѓ1.5Ј¬x2=3.5Ј»
ЈЁ4Ј©ЎЯa=©Ѓ1Ј¬b=3Ј¬
Ўа|x©Ѓa|+|x©Ѓb|=|x©ЃЈЁ©Ѓ1Ј©|+|x©Ѓ3|=|x+1|+|x©Ѓ3|Ј¬
µ±xЈѕ3К±Ј¬|x+1|+|x©Ѓ3|=x+1+x©Ѓ3=2x©Ѓ2Јѕ4Ј¬
µ±©Ѓ1ЎЬxЎЬ3К±Ј¬|x+1|+|x©Ѓ3|=x+1+3©Ѓx=4Ј¬
µ±xЈј©Ѓ1К±Ј¬|x+1|+|x©Ѓ3|=©Ѓx©Ѓ1+3©Ѓx=©Ѓ2x+2Јѕ4Ј¬
Ўа|x+1|+|x©Ѓ3|µДЧоРЎЦµКЗ4Ј¬
№Кґр°ёОЄЈє4Ј»
ЈЁ5Ј©Йиt·ЦЦУК±µгPµЅµгAЎўµгBµДѕаАлПаµИЈ¬
©Ѓt©ЃЈЁ©Ѓ1©Ѓ5tЈ©=t+3Ј¬
ЅвµГЈ¬t=![]() Ј¬
Ј¬
ґрЈє![]() ·ЦЦУК±µгPµЅµгAЎўµгBµДѕаАлПаµИЈ®
·ЦЦУК±µгPµЅµгAЎўµгBµДѕаАлПаµИЈ®


 Н¬ІЅЗбЛЙБ·П°ПµБРґр°ё
Н¬ІЅЗбЛЙБ·П°ПµБРґр°ё їОїОНЁїОіМ±кЧјЛјО¬·Ѕ·ЁУлДЬБ¦СµБ·ПµБРґр°ё
їОїОНЁїОіМ±кЧјЛјО¬·Ѕ·ЁУлДЬБ¦СµБ·ПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
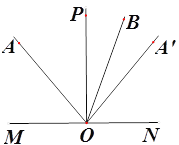
ЎѕМвДїЎїИзНјЈ¬ЖЅГжДЪТ»¶ЁµгAФЪЦ±ПЯMNµДЙП·ЅЈ¬µгOОЄЦ±ПЯMNЙПТ»¶Їµг Ј¬ЧчЙдПЯOAЎўOPЎўOAЎЇЈ¬µ±µгOФЪЦ±ПЯMNЙПФЛ¶ЇК±Ј¬КјЦХ±ЈіЦЎПMOP=90ЎгЎўЎПAOP=ЎПAЎЇOPЈ¬Ѕ«ЙдПЯOAИЖµгOЛіК±ХлРэЧЄ60ЎгµГµЅЙдПЯOB
ЈЁ1Ј©ИзНјЈ¬µ±µгOФЛ¶ЇµЅК№µгAФЪЙдПЯOPµДЧуІаЈ¬ИфOBЖЅ·ЦЎПAЎЇOPЈ¬ЗуЎПAOPµД¶ИКэЈ»
ЈЁ2Ј©µ±µгOФЛ¶ЇµЅК№µгAФЪЙдПЯOPµДЧуІаЈ¬ЎПAOM=3ЎПAЎЇOBК±Ј¬Зу![]() µДЦµЈ»
µДЦµЈ»
ЈЁ3Ј©µ±µгOФЛ¶ЇµЅДіТ»К±їМК±Ј¬ЎПAЎЇOB=150ЎгЈ¬Ц±ЅУРґіцЎПBOP= ¶И.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјКЗДіµҐФЄВҐѕУГсБщФВ·ЭµДУГµз(µҐО»Јє¶И)ЗйїцЈ¬Фт№ШУЪУГµзБїГиКцІ»ХэИ·µДКЗ(ЎЎЎЎ)
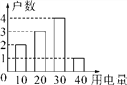
A. ЦЪКэОЄ30 B. ЦРО»КэОЄ30 C. ЖЅѕщКэОЄ24 D. ·ЅІоОЄ84
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїПВБРЛµ·ЁЈєўЩИф![]() =©Ѓ1Ј¬ФтaЎўb»ҐОЄПа·ґКэЈ»ўЪИфa+bЈј0Ј¬ЗТ
=©Ѓ1Ј¬ФтaЎўb»ҐОЄПа·ґКэЈ»ўЪИфa+bЈј0Ј¬ЗТ![]() Јѕ0Ј¬Фт|a+2b|=©Ѓa©Ѓ2bЈ»ўЫТ»ёцКэµДБў·ЅКЗЛь±ѕЙнЈ¬ФтХвёцКэОЄ0»т1Ј»ўЬИф©Ѓ1ЈјaЈј0Ј¬Фтa2Јѕ©Ѓ
Јѕ0Ј¬Фт|a+2b|=©Ѓa©Ѓ2bЈ»ўЫТ»ёцКэµДБў·ЅКЗЛь±ѕЙнЈ¬ФтХвёцКэОЄ0»т1Ј»ўЬИф©Ѓ1ЈјaЈј0Ј¬Фтa2Јѕ©Ѓ![]() Ј»ўЭИфa+b+cЈј0Ј¬abЈѕ0Ј¬cЈѕ0Ј¬Фт|©Ѓa|=©ЃaЈ¬ЖдЦРХэИ·µДёцКэКЗЈЁЎЎЎЎЈ©
Ј»ўЭИфa+b+cЈј0Ј¬abЈѕ0Ј¬cЈѕ0Ј¬Фт|©Ѓa|=©ЃaЈ¬ЖдЦРХэИ·µДёцКэКЗЈЁЎЎЎЎЈ©
A. 2ёц B. 3ёц C. 4ёц D. 5ёц
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїјЖЛгЈє
ЈЁ1Ј©![]() ЈЁ2Ј©
ЈЁ2Ј©![]()
ЈЁ3Ј©(Ј2![]() )Ј(Ј«4.7)Ј(Ј0.4)Ј« (Ј3.3) ЈЁ4Ј©
)Ј(Ј«4.7)Ј(Ј0.4)Ј« (Ј3.3) ЈЁ4Ј©![]()
ЈЁ5Ј©![]() ЈЁ6Ј©ЈЁ
ЈЁ6Ј©ЈЁ![]() -
-![]() +
+![]() Ј©ЎБЈЁ-36Ј©
Ј©ЎБЈЁ-36Ј©
ЈЁ7Ј©![]() ЈЁ8Ј©ЎЄ
ЈЁ8Ј©ЎЄ![]() (УГјт±г·Ѕ·ЁјЖЛг)
(УГјт±г·Ѕ·ЁјЖЛг)
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЎчABCЦРЈ¬AB=AC=10cmЈ¬BDЎНACУЪµгDЈ¬BD=8cmЈ®µгMґУµгAіц·ўЈ¬СШACµД·ЅПтФИЛЩФЛ¶ЇЈ¬Н¬К±Ц±ПЯPQУЙµгBіц·ўЈ¬СШBAµД·ЅПтФИЛЩФЛ¶ЇЈ¬ФЛ¶Ї№эіМЦРКјЦХ±ЈіЦPQЎОACЈ¬Ц±ПЯPQЅ»ABУЪµгPЎўЅ»BCУЪµгQЎўЅ»BDУЪµгFЈ®Б¬ЅУPMЈ¬ЙиФЛ¶ЇК±јдОЄtГлЈЁ0ЈјtЎЬ5Ј©Ј®ПЯ¶ОCMµДі¤¶ИјЗЧчyјЧ Ј¬ ПЯ¶ОBPµДі¤¶ИјЗЧчyТТ Ј¬ yјЧєНyТТ№ШУЪК±јдtµДєЇКэ±д»ЇЗйїцИзНјЛщКѕЈ®
ЈЁ1Ј©УЙНј2їЙЦЄЈ¬µгMµДФЛ¶ЇЛЩ¶ИКЗГїГл cmЈ¬µ±tОЄєОЦµК±Ј¬ЛД±ЯРОPQCMКЗЖЅРРЛД±ЯРОЈїФЪНј2ЦР·ґУіХвТ»ЗйїцµДµгКЗЈ»
ЈЁ2Ј©ЙиЛД±ЯРОPQCMµДГж»эОЄycm2 Ј¬ ЗуyУлtЦ®јдµДєЇКэ№ШПµКЅЈ»
ЈЁ3Ј©КЗ·сґжФЪДіТ»К±їМtЈ¬К№SЛД±ЯРОPQCM= ![]() SЎчABCЈїИфґжФЪЈ¬ЗуіцtµДЦµЈ»ИфІ»ґжФЪЈ¬ЛµГчАнУЙЈ»
SЎчABCЈїИфґжФЪЈ¬ЗуіцtµДЦµЈ»ИфІ»ґжФЪЈ¬ЛµГчАнУЙЈ»
ЈЁ4Ј©Б¬ЅУPCЈ¬КЗ·сґжФЪДіТ»К±їМtЈ¬К№µгMФЪПЯ¶ОPCµДґ№Ц±ЖЅ·ЦПЯЙПЈїИфґжФЪЈ¬ЗуіцґЛК±tµДЦµЈ»ИфІ»ґжФЪЈ¬ЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ТСЦЄA1(1Ј¬0)Ј¬A2(1Ј¬1)Ј¬A3(Ј1Ј¬1)Ј¬A4(Ј1Ј¬Ј1)Ј¬A5(2Ј¬Ј1)Ј¬ЎЈ¬ФтµгA2 019µДЧш±кОЄ____________Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїАоͬѧÿМмЙПС§Ўў·ЕС§К№УГ№«Ѕ»їЁіЛЧш№«Ѕ»іµЈ¬№«Ѕ»їЁµДУа¶оКЗ100ФЄЈ®Из№ыіЛіµґОКэУГ![]() ±нКѕЈ¬№«Ѕ»їЁЙПµДУа¶оУГ
±нКѕЈ¬№«Ѕ»їЁЙПµДУа¶оУГ![]() ±нКѕЈ®
±нКѕЈ®
ґОКэ | Уа¶о |
1 |
|
2 |
|
3 |
|
Ў | Ў |
(1)ЗлДгёщѕЭ±нёсЦРµДРЕПўЈ¬јЖЛгіцµЪ4ґОіЛіµєуЈ¬№«Ѕ»їЁЙПµДУа¶оЈ»
(2)ЗлДгРґіцАоН¬С§№«Ѕ»їЁЙПµДУа¶о![]() УліЛіµґОКэ
УліЛіµґОКэ![]() µД№ШПµКЅЈ»
µД№ШПµКЅЈ»
(3)Зл°пАоН¬С§јЖЛгіЛ20ґОіµєуЈ¬№«Ѕ»їЁЙПУа¶оКЗ¶аЙЩФЄЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЎчABCЦРЈ¬AB=AC=10Ј¬µгDКЗ±ЯBCЙПТ»¶Їµг ЈЁІ»УлBЈ¬CЦШєПЈ©Ј¬ЎПADE=ЎПB=¦БЈ¬DEЅ»ACУЪµгEЈ¬ЗТ ![]() Ј®ПВБРЅбВЫЈє ўЩЎчADEЎЧЎчACDЈ»
Ј®ПВБРЅбВЫЈє ўЩЎчADEЎЧЎчACDЈ»
ўЪµ±BD=6К±Ј¬ЎчABDУлЎчDCEИ«µИЈ»
ўЫЎчDCEОЄЦ±ЅЗИэЅЗРОК±Ј¬BDОЄ8»т ![]() Ј»
Ј»
ўЬCD2=CECAЈ®
ЖдЦРХэИ·µДЅбВЫКЗЈЁ°СДгИПОЄХэИ·ЅбВЫµДРтєЕ¶јМоЙПЈ©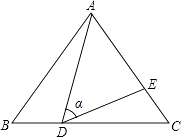
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com