
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,BD=8cm.点M从点A出发,沿AC的方向匀速运动,同时直线PQ由点B出发,沿BA的方向匀速运动,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t≤5).线段CM的长度记作y甲 , 线段BP的长度记作y乙 , y甲和y乙关于时间t的函数变化情况如图所示.
(1)由图2可知,点M的运动速度是每秒 cm,当t为何值时,四边形PQCM是平行四边形?在图2中反映这一情况的点是;
(2)设四边形PQCM的面积为ycm2 , 求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PQCM= ![]() S△ABC?若存在,求出t的值;若不存在,说明理由;
S△ABC?若存在,求出t的值;若不存在,说明理由;
(4)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
【答案】
(1)解:2;E( ![]() ,
, ![]() )
)
(2)
解:∵PQ∥AC,
∴△PBQ∽△ABC,
∴△PBQ为等腰三角形,PQ=PB=t,
∴ ![]() ,即
,即 ![]() ,
,
解得:BF= ![]() t,
t,
∴FD=BD﹣BF=8﹣ ![]() t,
t,
又∵MC=AC﹣AM=10﹣2t,
∴y= ![]() (PQ+MC)FD=
(PQ+MC)FD= ![]() (t+10﹣2t)(8﹣
(t+10﹣2t)(8﹣ ![]() t)=
t)= ![]() t2﹣8t+40
t2﹣8t+40
(3)
解:存在;
∵S△ABC= ![]() ACBD=
ACBD= ![]() ×10×8=40,
×10×8=40,
当S四边形PQCM= ![]() S△ABC时,y=
S△ABC时,y= ![]() t2﹣8t+40=20,
t2﹣8t+40=20,
解得:t=10﹣5 ![]() ,或t=10+5
,或t=10+5 ![]() (不合题意,舍);
(不合题意,舍);
即:t=10﹣5 ![]() 时,S四边形PQCM=
时,S四边形PQCM= ![]() S△ABC
S△ABC
(4)
解:假设存在某一时刻t,使得M在线段PC的垂直平分线上,则MP=MC,
过M作MH⊥AB,交AB与H,如图所示:
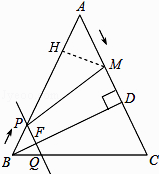
∵∠A=∠A,∠AHM=∠ADB=90°,
∴△AHM∽△ADB,
∴ ![]() ,
,
又∵AD=6,
∴ ![]() ,
,
∴HM= ![]() t,AH=
t,AH= ![]() t,
t,
∴HP=10﹣t﹣ ![]() t=10﹣
t=10﹣ ![]() t,
t,
在Rt△HMP中,MP2=( ![]() t)2+(10﹣
t)2+(10﹣ ![]() t)2=
t)2= ![]() t2﹣44t+100,
t2﹣44t+100,
又∵MC2=(10﹣2t)2=100﹣40t+4t2,
∵MP2=MC2,
∴ ![]() t2﹣44t+100=100﹣40t+4t2,
t2﹣44t+100=100﹣40t+4t2,
解得 t1= ![]() ,t2=0(舍去),
,t2=0(舍去),
∴t= ![]() s时,点M在线段PC的垂直平分线上.
s时,点M在线段PC的垂直平分线上.
【解析】解:(1)由图2得,点M的运动速度为2cm/s,PQ的运动速度为1cm/s,
∵四边形PQCM是平行四边形,则PM∥QC,
∴AP:AB=AM:AC,
∵AB=AC,
∴AP=AM,即10﹣t=2t,
解得:t= ![]() ,
,
∴当t= ![]() 时,四边形PQCM是平行四边形,此时,图2中反映这一情况的点是E(
时,四边形PQCM是平行四边形,此时,图2中反映这一情况的点是E( ![]() ,
, ![]() )
)
所以答案是:2,E( ![]() ,
, ![]() ).
).
【考点精析】通过灵活运用相似三角形的应用,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )

A. ①②④ B. ②③④
C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( ) ①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.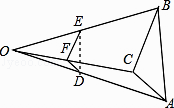
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m),在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(-3,1),B(-3,-3),第三个景点C(3,2)的位置已破损.
(1)请在图中标出景点C的位置;
(2)小明想从景点B开始游玩,途经景点A,最后到达景点C,求小明一家最短的行走路程(参考数据:![]() ≈6,结果保留整数).
≈6,结果保留整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:数轴上有A、B两点,分别对应的数为a,b,已知(a+1)2与|b﹣3|互为相反数.点P为数轴上一动点,对应为x.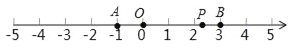
(1)a= ;b=
(2)若点P到点A和点B的距离相等,则点P对应的数是
(3)数轴上是否存在点P,使点P到点A和点B的距离之和为5?若存在,请求出x的值;若不存在,说明理由;
(4)|x﹣a|+|x﹣b|的最小值=
(5)当点P以每分钟1个单位长度的速度从O点向左运动,点A以每分钟5个单位长度向左运动,问几分钟时点P到点A、点B的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
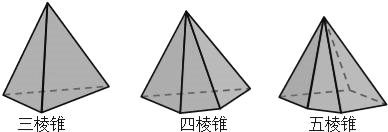
【题目】设棱锥的顶点数为V,面数为F,棱数为E.
(1)观察与发现:三棱锥中,V3= ,F3= ,E3= ;
五棱锥中,V5= ,F5= ,E5= ;
(2)猜想:①十棱锥中,V10= ,F10= ,E10= ;
②n棱锥中,Vn= ,Fn= ,En= ;(用含有n的式子表示)
(3)探究:①棱锥的顶点数(V)与面数(F)之间的等量关系: ;
②棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系:E= ;
(4)拓展:棱柱的顶点数(V)、面数(F)、棱数(E)之间是否也存在某种等量关系?若存在,试写出相应的等式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
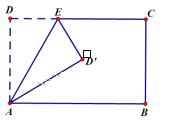
【题目】如图,矩形ABCD中,AB=8,AD=5,点E![]() 为DC边上一个动点,把△ADE沿AE折叠,点D的对应点D’落在矩形ABCD的对称轴上时,DE的长为____________.
为DC边上一个动点,把△ADE沿AE折叠,点D的对应点D’落在矩形ABCD的对称轴上时,DE的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到1h;②A,B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1小时后与摩托车相遇,此时距B地40千米.其中正确结论的个数是( )
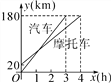
A. 2个 B. 3个 C. 4个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,E为AB上一点,将△BCE沿CE翻折至△FCE,EF与AD相交于点G,且AG=FG,则线段AE的长为______.
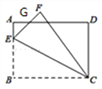
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com