
【题目】某商场计划投入一笔资金采购一批紧俏商品,经过市场调查发现,如果月初出售,可获利15﹪,并可用本金和利润再投资其他商品,到月末又可获利10﹪;如果月末出售可获利30﹪,但要付出仓储费用700元.
(1)若商场投资![]() 元,分别用含
元,分别用含![]() 的代数式表示月初出售和月末出售所获得的利润;
的代数式表示月初出售和月末出售所获得的利润;
(2)若商场投资40000元,问选择哪种销售方式获利较多?此时获利多少元?
【答案】(1)0.265x;0.3x-700;(2)月末出售所获得的利润较多,此时获利11300元.
【解析】试题分析:(1)根据题意可以用代数式表示出月初月末两种销售方式获得的利润;
(2)将x=40000分别代入(1)中的代数式,然后比较,即可解答本题.
试题解析:(1)由题意可得,
该商月初出售时的利润为:15%x+x(1+15%)×10%=0.265x(元),
该商月末出售时的利润为:30%x-700=(0.3x-700)(元);
(2)当x=40000时,
该商月初出售时的利润为:0.265×40000=10600(元),
该商月末出售时的利润为:0.3×40000-700=11300(元),
∵11300>10600,
∴选择月末出售这种方式,
即若商场投资40000元,选择月末销售方式获利较多,此时获利11300元.


科目:初中数学 来源: 题型:
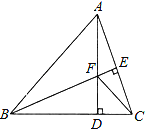
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,点D在CE上,AF⊥CB,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:CE=2AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年来全国各省市市政府民生实事之一的公共自行车建设工作已基本完成,网上资料显示呼和浩特市某部门对14年4月份中的7天进行了公共自行车日租车辆的统计,结果如图: 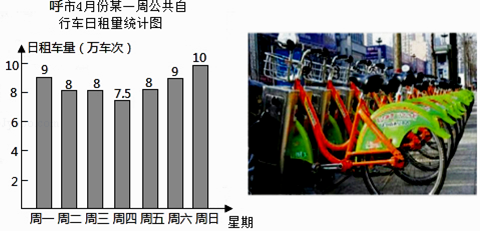
(1)求这7天日租车量的众数、中位数和平均数;
(2)用(1)中的平均数估计4月份(30天)该市共租车多少万车次;
(3)资料显示,呼市政府在公共自行车建设项目中共投入9600万元,估计2014年共租车3200万车次,每车次平均收入租车费0.1元,求2014年该市租车费收入占总投入的百分率(精确到0.1%).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,□ABCD的对角线AC,BD相交于点O,E、F、G、H分别是OA、OB、OC、OD的中点,那么□ABCD与四边形EFGH是否是位似图形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为控制禽流感病毒传播,某地关闭活禽交易市场,冷冻鸡肉销量上升,某公司在春节期间采购冷冻鸡肉60箱销往城市和乡镇,已知冷冻鸡肉在城市销售平均每箱的利润y1(百元)与销售数量x(箱)的关系为y1= 在乡镇销售平均每箱的利润y2(百元)与销售数量t(箱)的关系为y2=
在乡镇销售平均每箱的利润y2(百元)与销售数量t(箱)的关系为y2=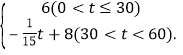
(1)t与x的关系是 ,将y2转换为x为自变量的函数,则y2= ;
(2)设春节期间售完全部冷冻鸡肉可获得总利润W(百元),当在城市销售量x(箱)的范围是0<x≤20时,求W与x的关系式(总利润=在城市销售利润+在乡镇销售利润);
(3)经测算,在20<x≤30的范围内,可以获得最大总利润,求这个最大总利润,并求出此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D是AB上的一个动点(不与A、B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况是( )
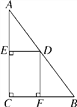
A. 逐渐减小 B. 逐渐增大 C. 先增大后减小 D. 先减小后增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道:|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
![]()
(1)数轴上表示5与﹣2两点之间的距离是
(2)数轴上表示x与2的两点之间的距离可以表示为 .
(3)同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+3|+|x﹣1|=4,这样的整数是 .
(4)由以上探索猜想|x+10|+|x+2|+|x﹣8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
(5)由以上探索猜想|x+10|+|x+2|+|x﹣8|+|x﹣10|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
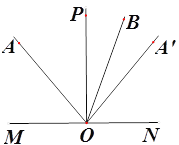
【题目】如图,平面内一定点A在直线MN的上方,点O为直线MN上一动点 ,作射线OA、OP、OA’,当点O在直线MN上运动时,始终保持∠MOP=90°、∠AOP=∠A’OP,将射线OA绕点O顺时针旋转60°得到射线OB
(1)如图,当点O运动到使点A在射线OP的左侧,若OB平分∠A’OP,求∠AOP的度数;
(2)当点O运动到使点A在射线OP的左侧,∠AOM=3∠A’OB时,求![]() 的值;
的值;
(3)当点O运动到某一时刻时,∠A’OB=150°,直接写出∠BOP= 度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com