
【题目】为控制禽流感病毒传播,某地关闭活禽交易市场,冷冻鸡肉销量上升,某公司在春节期间采购冷冻鸡肉60箱销往城市和乡镇,已知冷冻鸡肉在城市销售平均每箱的利润y1(百元)与销售数量x(箱)的关系为y1= 在乡镇销售平均每箱的利润y2(百元)与销售数量t(箱)的关系为y2=
在乡镇销售平均每箱的利润y2(百元)与销售数量t(箱)的关系为y2=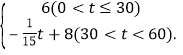
(1)t与x的关系是 ,将y2转换为x为自变量的函数,则y2= ;
(2)设春节期间售完全部冷冻鸡肉可获得总利润W(百元),当在城市销售量x(箱)的范围是0<x≤20时,求W与x的关系式(总利润=在城市销售利润+在乡镇销售利润);
(3)经测算,在20<x≤30的范围内,可以获得最大总利润,求这个最大总利润,并求出此时x的值.
【答案】(1)t=60-x 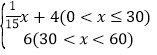 (2)W=
(2)W=![]() x2+5x+240; (3) 382.5百元
x2+5x+240; (3) 382.5百元
【解析】(1)直接利用采购冷冻鸡肉60箱销往城市和乡镇,表示出t与x的关系即可,进而代入y2求出即可;
(2)利用(1)中所求结合自变量取值范围得出W与x的函数关系式即可;
(3)利用(1)中所求结合自变量取值范围得出W与x的函数关系式,进而利用函数增减性求出函数最值即可.
(1)∵某公司在春节期间采购冷冻鸡肉60箱销往城市和乡镇,在城市销售数量x(箱),
∴在乡镇销售数量t(箱)的关系为:t=60-x,
∴y2=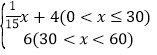 ,
,
故答案为:t=60-x,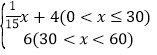 ;
;
(2)综合y1=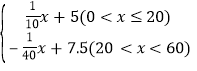 和(1)中 y2,当对应的x范围是0<x≤20 时,
和(1)中 y2,当对应的x范围是0<x≤20 时,
W=![]() x+
x+![]() (60-x)=
(60-x)=![]() x2+5x+240;
x2+5x+240;
(3)当20<x≤30时,
W=![]() x+
x+![]() (60-x)=-
(60-x)=-![]() x2+7.5x+240,
x2+7.5x+240,
∵x=-![]() =
=![]() >30,
>30,
∴在20<x≤30的范围内W随x的增大而增大,
∴当x=30时,W有最大值,W最大=-![]() ×302+7.5×30+240=382.5(百元).
×302+7.5×30+240=382.5(百元).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA延长线于点E,点F是DE延长线上一点,连接AF. 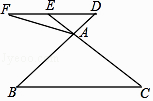
(1)如果 ![]() =
= ![]() ,DE=6,求边BC的长;
,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用棋子摆成的“上”字:

第一个“上”字 第二个“上”字 第三个“上”字
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第四、第五个“上”字分别需用 和 枚棋子.
(2)第n个“上”字需用 枚棋子.
(3)如果某一图形共有102枚棋子,你知道它是第几个“上”字吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划投入一笔资金采购一批紧俏商品,经过市场调查发现,如果月初出售,可获利15﹪,并可用本金和利润再投资其他商品,到月末又可获利10﹪;如果月末出售可获利30﹪,但要付出仓储费用700元.
(1)若商场投资![]() 元,分别用含
元,分别用含![]() 的代数式表示月初出售和月末出售所获得的利润;
的代数式表示月初出售和月末出售所获得的利润;
(2)若商场投资40000元,问选择哪种销售方式获利较多?此时获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学在沙滩上用石子摆成的小房子

观察图形的变化规律,则第10个小房子用了( )颗石子.
A. 119 B. 121 C. 140 D. 142
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司派出甲车前往某地完成任务,此时,有一辆流动加油车与他同时出发,且在同一条公路上匀速行驶(速度保持不变).为了确定汽车的位置,我们用OX表示这条公路,原点O为零千米路标,并作如下约定:速度为正,表示汽车向数轴的正方向行驶;速度为负,表示汽车向数轴的负方向行驶;速度为零,表示汽车静止.行程为正,表示汽车位于零千米的右侧;行程为负,表示汽车位于零千米的左侧;行程为零,表示汽车位于零千米处.两车行程记录如表:

由上面表格中的数据,解决下列问题:
(1)甲车开出7小时时的位置为 km,流动加油车出发位置为 km;
(2)当两车同时开出x小时时,甲车位置为 km,流动加油车位置为 km (用x的代数式表示);
(3)甲车出发前由于未加油,汽车启动后司机才发现油箱内汽油仅够行驶3小时,问:甲车连续行驶3小时后,能否立刻获得流动加油车的帮助?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )

A. ①②④ B. ②③④
C. ①②③ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com