
【题目】已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点F,连接ED,且有ED=EF. 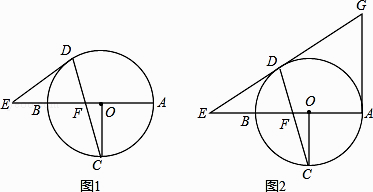
(1)如图1,求证:ED为⊙O的切线;
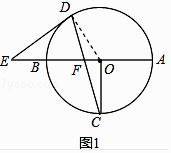
(2)如图2,直线ED与切线AG相交于G,且OF=2,⊙O的半径为6,求AG的长.
【答案】
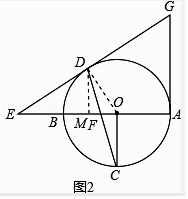
(1)证明:连接OD,
∵ED=EF,
∴∠EDF=∠EFD,
∵∠EFD=∠CFO,
∴∠EDF=∠CFO.
∵OD=OC,
∴∠ODF=∠OCF.
∵OC⊥AB,
∴∠CFO+∠OCF=∠EDF+∠ODF=∠EDO=90°,
∴ED为⊙O的切线
(2)解:连接OD,过点D作DM⊥BA于点M,
由(1)可知△EDO为直角三角形,设ED=EF=a,EO=EF+FO=a+2,
由勾股定理得,EO2=ED2+DO2,即(a+2)2=a2+62,
解得,a=8,即ED=8,EO=10.
∵sin∠EOD= ![]() =
= ![]() ,cos∠EOD=
,cos∠EOD= ![]() =
= ![]() ,
,
∴DM=ODsin∠EOD=6× ![]() =
= ![]() ,MO=ODcos∠EOD=6×
,MO=ODcos∠EOD=6× ![]() =
= ![]() ,
,
∴EM=EO﹣MO=10﹣ ![]() =
= ![]() ,EA=EO+OA=10+6=16.
,EA=EO+OA=10+6=16.
∵GA切⊙O于点A,
∴GA⊥EA,
∴DM∥GA,
∴△EDM∽△EGA,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,GA=12.
【解析】(1)连接OD,由ED=EF可得出∠EDF=∠EFD,由对顶角相等可得出∠EDF=∠CFO;由OD=OC可得出∠ODF=∠OCF,结合OC⊥AB即可得知∠EDF+∠ODF=90°,即∠EDO=90°,由此证出ED为⊙O的切线;(2)连接OD,过点D作DM⊥BA于点M,结合(1)的结论根据勾股定理可求出ED、EO的长度,结合∠DOE的正弦、余弦值可得出DM、MO的长度,根据切线的性质可知GA⊥EA,从而得出DM∥GA,根据相似三角形的判定定理即可得出△EDM∽△EGA,根据相似三角形的性质即可得出GA的长度


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的重量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准重量的差值(单位:g) | ﹣5 | ﹣2 | 0 | 1 | 3 | 6 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)计算这批样品的平均重量,判断它比标准重量重还是轻多少?
(2)若标准重量为450克,则这批样品的总重量是多少?
(3)若这种食品的合格标准为450±5克,则这批样品的合格率为 (直接填写答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盛盛同学到某高校游玩时,看到运动场的宣传栏中的部分信息(如下表):
院系篮球赛成绩公告 | |||
比赛场次 | 胜场 | 负场 | 积分 |
22 | 12 | 10 | 34 |
22 | 14 | 8 | 36 |
22 | 0 | 22 | 22 |
盛盛同学结合学习的知识设计了如下问题,请你帮忙完成下列问题:
(1)从表中可以看出,负一场积______分,胜一场积_______分;
(2)某队在比完22场的前提下,胜场总积分能等于其负场总积分的2倍吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知[x]表示不超过x的最大整数,如[3]=3;[3.14]=3;[﹣3.14]=﹣4.
根据以上规则解答下列问题:
(1)[﹣8]= ;[5.4]= ;[﹣6.99]= ;
(2)若[x]=﹣5,则x的范围是 ;
(3)已知正整数n小于100,![]() =n﹣2,求所有满足条件正整数n.
=n﹣2,求所有满足条件正整数n.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图像如图所示,图像过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣ ![]() ,y2)、点C(
,y2)、点C( ![]() ,y3)在该函数图像上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 其中正确的结论有( )
,y3)在该函数图像上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 其中正确的结论有( )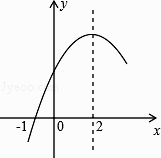
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
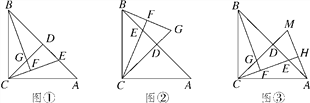
【题目】如图①,在△ABC中,AC=BC,∠ACB=90°,过点C作CD⊥AB于点D,点E是AB边上一动点(不含端点A,B),连接CE,过点B作CE的垂线交直线CE于点F,交直线CD于点G.
(1)求证:AE=CG;
(2)若点E运动到线段BD上时(如图②),试猜想AE,CG的数量关系是否发生变化,请写出你的结论;
(3)过点A作AH⊥CE,垂足为点H,并交CD的延长线于点M(如图③),找出图中与BE相等的线段,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=﹣x2+bx+c经过原点O和点P,已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).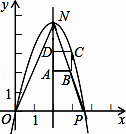
(参考公式:y=ax2+bx+c(a≠0)的顶点坐标是(﹣ ![]() ,
, ![]() ).
).
(1)若当n=4时求c,b并写出抛物线对称轴及y的最大值;
(2)求证:抛物线的顶点在函数y=x2的图像上;
(3)若抛物线与直线AD交于点N,求n为何值时,△NPO的面积为1;
(4)若抛物线经过正方形区域ABCD(含边界),请直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b是多项式2m2n﹣m3n2﹣m﹣2的次数,c是单项式﹣2xy2的系数,且a、b、c分别是点A、B、C在数轴上对应的数.
![]()
(1)求a、b、c的值,并在数轴上标出点A、B、C.
(2)若M点在此在此数轴上运动,请求出M点到AB两点距离之和的最小值;
(3)若动点P、Q同时从A、B出发沿数轴负方向运动,点P的速度是每秒![]() 个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q能追上点P?
个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q能追上点P?
(4)在数轴上找一点N,使点M到A、B、C三点的距离之和等于10,请直接写出所有的N对应的数.(不必说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com