
【题目】如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=﹣x2+bx+c经过原点O和点P,已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).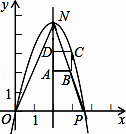
(参考公式:y=ax2+bx+c(a≠0)的顶点坐标是(﹣ ![]() ,
, ![]() ).
).
(1)若当n=4时求c,b并写出抛物线对称轴及y的最大值;
(2)求证:抛物线的顶点在函数y=x2的图像上;
(3)若抛物线与直线AD交于点N,求n为何值时,△NPO的面积为1;
(4)若抛物线经过正方形区域ABCD(含边界),请直接写出n的取值范围.
【答案】
(1)
解:当n=4时,则P(4,0),
∵抛物线y=﹣x2+bx+c经过原点O和点P,
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=﹣x2+4x=﹣(x﹣2)2+4,
∴抛物线对称轴为直线x=2,
∵﹣1<0,
∴当x=2时,y有最大值4
(2)
证明:把O、P的坐标代入抛物线解析式可得 ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=﹣x2+nx=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
∴抛物线顶点坐标为( ![]() ,
, ![]() ),
),
在y=x2中,当x= ![]() 时,y=
时,y= ![]() ,
,
∴抛物线的顶点在函数y=x2的图像上
(3)
解:在y=﹣x2+nx中,当x=2时,y=2n﹣4,
∴N点坐标为(2,2n﹣4),
∴N到x轴的距离为|2n﹣4|=2|n﹣2|,
∵P(n,0),
∴OP=n,
∴S△NPO= ![]() n×2|n﹣2|=n|n﹣2|,
n×2|n﹣2|=n|n﹣2|,
当△NPO的面积为1时,则有n|n﹣2|=1,
当n=2时,N、P重合,不成立,
当n>2时,则n2﹣2n=1,解得n=1+ ![]() 或n=1﹣
或n=1﹣ ![]() (此时n小于2,舍去),
(此时n小于2,舍去),
当0<n<2时,则2n﹣n2=1,解得n1=n2=1,
综上可知当n的值为1+ ![]() 或1时,△NPO的面积为1
或1时,△NPO的面积为1
(4)
解:∵抛物线解析式为y=﹣x2+nx,
∴当过A(2,2)时,代入可得2=﹣4+2n,解得n=3,
同理当抛物线过B时可求得n= ![]() ,当抛物线过点C时可求得n=4,当抛物线过点D时可求得n=
,当抛物线过点C时可求得n=4,当抛物线过点D时可求得n= ![]() ,
,
∴n的取值范围为3≤n≤4
【解析】(1)把原点和P点坐标代入抛物线解析式可求得b、c,则可求得抛物线解析式,化为顶点式可求得其对称轴和最大值;(2)用n可表示出抛物线的解析式,则可求得其顶点坐标,代入y=x2进行验证即可;(3)可用n表示出N点坐标,则可表示出N到x轴的距离和OP的长,可表示出△NPO的面积,可得到关于n的方程,可求得n的值;(4)分别把A、B、C、D的坐标代入抛物线解析式可求得n的值,则可求得n的取值范围.


科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图像如图所示,根据图像所提供的信息解答下列问题: 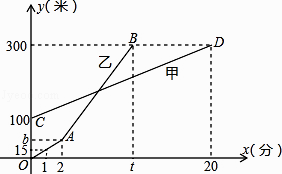
(1)甲登山上升的速度是每分钟米,乙在A地时距地面的高度b为米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)求该商店销售的乒乓球拍每副的标价.
(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:
①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点F,连接ED,且有ED=EF. 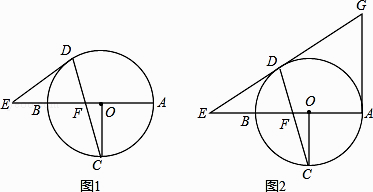
(1)如图1,求证:ED为⊙O的切线;
(2)如图2,直线ED与切线AG相交于G,且OF=2,⊙O的半径为6,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将一张正方形纸片剪成四个大小一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去。
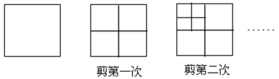
(1)完成下表:
剪的次数 | 1 | 2 | 3 | 4 | 5 | ... | n |
小正方形的个数 | 4 | 7 | 10 | ... |
|
(2)![]() .(用含n的代数式表示)
.(用含n的代数式表示)
(3)按上述方法,能否得到2018个小正方形?如果能,请求出n;如不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某单元楼居民六月份的用电(单位:度)情况,则关于用电量描述不正确的是( )
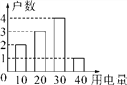
A. 众数为30 B. 中位数为30 C. 平均数为24 D. 方差为84
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设边长为3的正方形的对角线长为a.下列关于a的四种说法: ①a是无理数;
②a可以用数轴上的一个点来表示;
③3<a<4;
④a是18的算术平方根.
其中,所有正确说法的序号是( )
A.①④
B.②③
C.①②④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() (2)
(2)![]()
(3)(-2![]() )-(+4.7)-(-0.4)+ (-3.3) (4)
)-(+4.7)-(-0.4)+ (-3.3) (4)![]()
(5)![]() (6)(
(6)(![]() -
-![]() +
+![]() )×(-36)
)×(-36)
(7)![]() (8)—
(8)—![]() (用简便方法计算)
(用简便方法计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃容器高19cm,底面周长为60cm,在外侧距下底1.5cm的点A处有一只蜘蛛,在蜘蛛正对面的圆柱形容器的外侧,距上底1.5cm处的点B处有一只苍蝇,蜘蛛急于捕捉苍蝇充饥,请你帮蜘蛛计算它沿容器侧面爬行的最短距离.
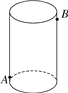
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com