
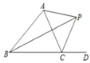
【题目】如图 ,△ABC 的外角平分线 CP 和内角平分线 BP 相交于点 P,若∠BPC=25°,则∠CAP=__________.
【答案】65°
【解析】
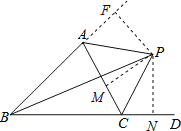
延长BA,作PN⊥BD于点N,PF⊥BA于点F,PM⊥AC于点M,设∠PCD=x°,根据外角与内角性质得出∠BAC的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP=∠FAP,即可得出答案.
延长BA,作PN⊥BD于点N,PF⊥BA于点F,PM⊥AC于点M,
设∠PCD=x°,
∵CP平分∠ACD,
∴∠ACP=∠PCD=x°,PM=PN,
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∵∠BPC=25°,
∴∠ABP=∠PBC=(x-25)°,
∴∠BAC=∠ACD-∠ABC=2x°-(x°-25°)-(x°-25°)=50°,
∴∠CAF=130°,
在Rt△PFA和Rt△PMA中,
![]()
∴Rt△PFA≌Rt△PMA(HL),
∴∠FAP=∠PAC=65°.
故答案为65°.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥BC,垂足为C,AC=2cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_____秒时,△BCA与点P、N、B为顶点的三角形全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技与经济的发展,中国廉价劳动力的优势开始逐渐消失,而作为新兴领域的机器人产业则迅速崛起,机器人自动化线的市场也越来越大,并且逐渐成为自动化生产线的主要方式,某化工厂要在规定时间内搬运1200千元化工原料.现有A,B两种机器人可供选择,已知A型机器人比B型机器人每小时多搬运30千克,A型机器人搬运900千克所用的时间与B型机器人搬运600千克所用的时间相等.


(1)两种机器人每小时分别搬运多少化工原料?
(2)该工厂原计划同时使用这两种机器人搬运,工作一段时间后,A型机器人又有了新的搬运任务,但必须保证这批化工原料在11小时内全部搬运完毕.求:A型机器人至少工作几个小时,才能保证这批化工原料在规定的时间内完成.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠A=∠D,说明∠F与∠C相等的理由.
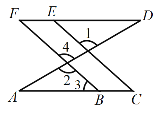
解:∵∠1=∠2( 已知 ),∠2=∠4 ( ),
∴∠1=∠4( 等量代换 ),
∴FB∥EC( ),
∴∠3=∠C( 两直线平行,同位角相等 ).
∵∠A=∠D( ),
∴ED∥AC( ),
∴∠F=∠3 ( ),
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y=![]() (x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为_____.
(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
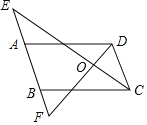
【题目】如图,已知∠DAE+∠CBF=180°,CE平分∠BCD,∠BCD=2∠E.
(1)求证:AD∥BC;
(2)CD与EF平行吗?写出证明过程;
(3)若DF平分∠ADC,求证:CE⊥DF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com