
【题目】随着科技与经济的发展,中国廉价劳动力的优势开始逐渐消失,而作为新兴领域的机器人产业则迅速崛起,机器人自动化线的市场也越来越大,并且逐渐成为自动化生产线的主要方式,某化工厂要在规定时间内搬运1200千元化工原料.现有A,B两种机器人可供选择,已知A型机器人比B型机器人每小时多搬运30千克,A型机器人搬运900千克所用的时间与B型机器人搬运600千克所用的时间相等.


(1)两种机器人每小时分别搬运多少化工原料?
(2)该工厂原计划同时使用这两种机器人搬运,工作一段时间后,A型机器人又有了新的搬运任务,但必须保证这批化工原料在11小时内全部搬运完毕.求:A型机器人至少工作几个小时,才能保证这批化工原料在规定的时间内完成.
【答案】(1)A型机器人每小时搬运90千克化工原料,B型机器人每小时搬运90千克化工原料;(2)A型机器人至少工作6小时,才能保证这批化工原料在规定的时间内完成.
【解析】(1)设B型机器人每小时搬运x千克化工原料,则A型机器人每小时搬运(x+30)千克化工原料,根据A型机器人搬运900千克所用的时间与B型机器人搬运600千克所用的时间相等建立方程求出其解就可以得出结论.
(2)设A型机器人工作t小时,根据这批化工原料在11小时内全部搬运完毕列出不等式并解答.
(1)设B型机器人每小时搬运x千克化工原料,则A型机器人每小时搬运(x+30)千克化工原料,
根据题意,得
![]() ,
,
解得x=60.
经检验,x=60是所列方程的解.
当x=60时,x+60=90.
答:A型机器人每小时搬运90千克化工原料,B型机器人每小时搬运90千克化工原料;
(2)设A型机器人工作t小时,
根据题意,得1200-90t≤60×11,
解得t≥6.
答:A型机器人至少工作6小时,才能保证这批化工原料在规定的时间内完成.


科目:初中数学 来源: 题型:
【题目】如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动,2秒后,两点相距16个单位长度,已知动点A、B的速度比为1:3(速度单位:1个单位长度秒).
![]()
(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,满足OB=2OA?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC在平面直角坐标系中的位置如图所示(图中每个小方格边长均为1个单位长度).
(1)求△ABC的面积.
(2)△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+3,y0﹣4),将△ABC作同样的平移得到△A1B1C1,写出A1、B1、C1的坐标.A1 ,B1 ,C1 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在 ABC 中,BAC 90° ,分别过顶点 B、C 作 A 点的直线的垂线垂足分别为 D、E,试探究线段 BD、CE、DE 之间的关系.
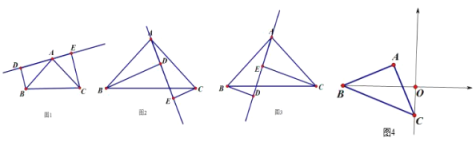
(1)当直线 DE 绕点 A 旋转至如图 1 的位置,直接写出 BD、CE、DE 之间的数量 为 ;
(2)当直线 DE 绕点 A 旋转至如图 2 的位置,直接写出 BD、CE、DE 之间的数量 为 ;
(3)当直线 DE 绕点 A 旋转至如图 3 的位置,写出 BD、CE、DE 之间的数量,并证明 你的结论;
(4)如图 4,如果将 ABC 放在直角坐标系中,若点 A 的坐标为(-1,1),求 OB-OC 的 值.请写出必要的解答步骤.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点D,E,F分别是△ABC的边AB,AC,BC上的点,DE∥BC,DF∥AC.
(1)如图1,点G是线段FD延长线上一点,连接EG,∠CEG的平分线EM交AB于点M,交FD于点N.则∠A,∠AME,∠CEG之间存在怎样的数量关系?请写出证明过程;
(2)如图2,在(1)的条件下,若EG平分∠AED,∠AME=35°,且∠EDF﹣∠A=30°,求∠C的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com