
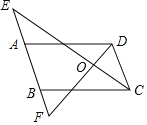
【题目】如图,已知∠DAE+∠CBF=180°,CE平分∠BCD,∠BCD=2∠E.
(1)求证:AD∥BC;
(2)CD与EF平行吗?写出证明过程;
(3)若DF平分∠ADC,求证:CE⊥DF.
【答案】(1)详见解析;(2)CD∥EF,证明详见解析;(3)详见解析.
【解析】
(1)根据同角的补角相等,即可得到∠CBF=∠DAB,进而得到AD∥BC;
(2)依据∠BCD=2∠DCE,∠BCD=2∠E,即可得出∠E=∠DCE,进而判定CD∥EF;
(3)依据AD∥BC,可得∠ADC+∠DCB=180°,进而得到∠COD=90°,即可得出CE⊥DF.
解:(1)∵∠DAE+∠CBF=180°,∠DAE+∠DAB=180°,
∴∠CBF=∠DAB,
∴AD∥BC;
(2)CD与EF平行.
∵CE平分∠BCD,
∴∠BCD=2∠DCE,
又∵∠BCD=2∠E,
∴∠E=∠DCE,
∴CD∥EF;
(3)∵DF平分∠ADC,
∴∠CDF=![]() ∠ADC,
∠ADC,
∵∠BCD=2∠DCE,
∴∠DCE=![]() ∠DCB,
∠DCB,
∵AD∥BC,
∴∠ADC+∠DCB=180°,
∴∠CDF+∠DCE=![]() (∠ADC+∠DCB)=90°,
(∠ADC+∠DCB)=90°,
∴∠COD=90°,
∴CE⊥DF.


科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
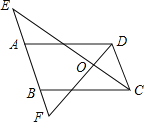
(1)如图1,当点D在线段BC上,如果∠BAC=90°,求∠BCE的度数;
(2)如图2,当点D在线段BC上,如果∠BAC=60°,则∠BCE的度数;
(3)设∠BAC=α,∠BCE=β,如图3,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点D,E,F分别是△ABC的边AB,AC,BC上的点,DE∥BC,DF∥AC.
(1)如图1,点G是线段FD延长线上一点,连接EG,∠CEG的平分线EM交AB于点M,交FD于点N.则∠A,∠AME,∠CEG之间存在怎样的数量关系?请写出证明过程;
(2)如图2,在(1)的条件下,若EG平分∠AED,∠AME=35°,且∠EDF﹣∠A=30°,求∠C的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠BAC=60°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作菱形ADEF,使∠DAF=60°,连接CF.
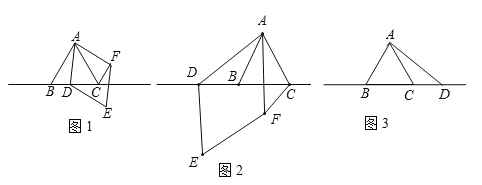
(1)观察猜想:如图1,当点D在线段BC上时,①AB与CF的位置关系为: ;
②BC,CD,CF之间的数量关系为: .
(2)数学思考:如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸:如图3,当点D在线段BC的延长线上时,设AD与CF相交于点G,若已知AB=4,CD=![]() AB,求AG的长.
AB,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学组织全校1000名学生进行了校园安全知识竞赛.为了解本次知识竞赛的成绩分布情况,从中随机抽取了部分学生的成绩(得分取正整数,满分为100分),并绘制了如图的频数分布表和频数分布直方图(不完整).
分组 | 频数 | 频率 |
50.5~60.5 | 10 | a |
60.5~70.5 | b | |
70.5~80.5 | 0.2 | |
80.5~90.5 | 52 | 0.26 |
90.5~100.5 | 0.37 | |
合计 | c | 1 |
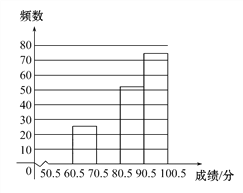
请根据以上提供的信息,解答下列问题:
(1)直接写出频数分布表中a,b,c的值,补全频数分布直方图.
(2)上述学生成绩的中位数落在哪一组范围内?
(3)学校将对成绩在90.5~100.5分之间的学生进行奖励,请估计全校1000名学生中约有多少名获奖?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com