
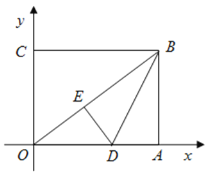
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角沿直线
的一个角沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
(1)求线段![]() 的长度;
的长度;
(2)求直线![]() 所对应的函数表达式;
所对应的函数表达式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)15;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据勾股定理即可解决问题;
(2)设AD=x,则OD=OA=AD=12-x,根据轴对称的性质,DE=x,BE=AB=9,又OB=15,可得OE=OB-BE=15-9=6,在Rt△OED中,根据OE2+DE2=OD2,构建方程即可解决问题;
(3)过点E作EP∥BD交BC于点P,过点P作PQ∥DE交BD于点Q,则四边形DEPQ是平行四边形,再过点E作EF⊥OD于点F,想办法求出最小PE的解析式即可解决问题.
解:(1)由题知:![]() .
.
(2)设![]() ,则
,则![]() ,
,
根据轴对称的性质,![]() ,
,![]() ,
,
又![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得 ![]() ,
,
∴![]() ,
,
∴点![]() ,
,
设直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]() ,
,
则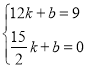 , 解得
, 解得![]() ,
,
∴直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]() ,
,
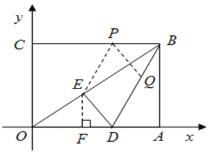
(3)存在,过点![]() 作EP∥DB交
作EP∥DB交![]() 于点
于点![]() ,过点
,过点![]() 作PQ∥ED交
作PQ∥ED交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是平行四边形.再过点
是平行四边形.再过点![]() 作
作![]() 于点
于点![]() ,
,
由![]() ,
,
得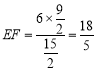 ,即点
,即点![]() 的纵坐标为
的纵坐标为![]() ,
,
又点![]() 在直线
在直线![]() :
:![]() 上,
上,
∴![]() , 解得
, 解得 ![]() , ∴
, ∴![]()
由于EP∥DB,所以可设直线![]() :
:![]() ,
,
∵![]() 在直线
在直线![]() 上
上
∴![]() , 解得
, 解得 ![]() ,
,
∴直线![]() :
:![]() ,
,
令![]() ,则
,则![]() ,
,
解得![]() ,
,
∴![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2)、B(2,0),C(4,2).
(1)在平面直角坐标系中画出△ABC;
(2)若将(1)中的△ABC平移,使点B的对应点B′坐标为(6,2),画出平移后的△A′B′C′;
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,AOBC的顶点A、C的坐标分别为A(﹣2,0)、C(0,3),反比例函数的图象经过点B.
(1)求反比例函数的表达式;
(2)这个反比例函数的图象与一个一次函数的图象交于点B、D(m,1),根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲,乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示,根据图象信息回答下列问题:
(分钟)之间的函数关系如图所示,根据图象信息回答下列问题:

(1)图书馆与学校之间的距离为 米;
(2)当![]() 分钟时,甲乙两人相遇;
分钟时,甲乙两人相遇;
(3)乙的速度为 米/分钟;
(4)![]() 点的坐标为 .
点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究发现
数学活动课上,小明说“若直线![]() 向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”
向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”
经过一番讨论,小组成员展示了他们的解答过程:
在直线![]() 上任取点
上任取点![]() ,
,
向左平移3个单位得到点![]()
设向左平移3个单位后所得直线所对应的函数表达式为![]() .
.
因为![]() 过点
过点![]() ,
,
所以![]() ,
,
所以![]() ,
,
填空:所以平移后所得直线所对应函数表达式为
(2)类比运用
已知直线![]() ,求它关于
,求它关于![]() 轴对称的直线所对应的函数表达式;
轴对称的直线所对应的函数表达式;
(3)拓展运用
将直线![]() 绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .
绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为边
为边![]() 上一点,
上一点,![]() 为边
为边![]() 的中点,过点
的中点,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连结
,连结![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若点![]() 为边
为边![]() 的中点,当线段BC与线段AC满足什么数量关系时,四边形
的中点,当线段BC与线段AC满足什么数量关系时,四边形![]() 为正方形.
为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠海市水务局对某小区居民生活用水情况进行了调査.随机抽取部分家庭进行统计,绘制成如下尚未完成的频数分布表和频率分布直方图.请根据图表,解答下列问题:
月均用水量(单位:吨 | 频数 | 频率 |
2≤x<3 | 4 | 0.08 |
3≤x<4 | a | b |
4≤x<5 | 14 | 0.28 |
5≤x<6 | 9 | c |
6≤x<7 | 6 | 0.12 |
7≤x<8 | 5 | 0.1 |
合计 | d | 1.00 |

(1)b= ,c= ,并补全频数分布直方图;
(2)为鼓励节约用水用水,现要确定一个用水量标准P(单位:吨),超过这个标准的部分按1.5倍的价格收费,若要使60%的家庭水费支出不受影响,则这个用水量标准P= 吨;
(3)根据该样本,请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com