
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲,乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示,根据图象信息回答下列问题:
(分钟)之间的函数关系如图所示,根据图象信息回答下列问题:

(1)图书馆与学校之间的距离为 米;
(2)当![]() 分钟时,甲乙两人相遇;
分钟时,甲乙两人相遇;
(3)乙的速度为 米/分钟;
(4)![]() 点的坐标为 .
点的坐标为 .
【答案】(1)2400;(2)24;(3)60;(4)![]()
【解析】
(1)根据图象可知图书馆与学校的距离即为甲乙两人开始时的距离2400米;
(2)当![]() 时,甲乙间的距离为0,即两人相遇;
时,甲乙间的距离为0,即两人相遇;
(3)根据图象可知甲的速度为![]() 米/分钟,甲、乙两人的速度和为
米/分钟,甲、乙两人的速度和为![]() 米/分钟;从而可得出乙的速度;
米/分钟;从而可得出乙的速度;
(4)乙从图书馆回学校的时间为![]() 分钟,
分钟,![]() ,即可得出点A的坐标.
,即可得出点A的坐标.
解:(1)根据图象可知图书馆与学校的距离即为甲乙两人开始时的距离2400米;
故答案为:2400;
(2)当![]() 时,甲乙间的距离为0,即两人相遇;
时,甲乙间的距离为0,即两人相遇;
故答案为:24;
(3)根据图象可知甲的速度为![]() 米/分钟,
米/分钟,
甲、乙两人的速度和为![]() 米/分钟,
米/分钟,
乙的速度为:![]() 米/分钟
米/分钟
故答案为:60;
(4)乙从图书馆回学校的时间为![]() 分钟,
分钟,![]() ,
,
∴点A的坐标为![]() .
.
故答案为:![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】发现:已知△ABC中,AE是△ABC的角平分线,∠B=72°,∠C=36°
(1)如图1,若AD⊥BC于点D,求∠DAE的度数;
(2)如图2,若P为AE上一个动点(P不与A、E重合),且PF⊥BC于点F时,∠EPF= °.
(3)探究:如图2△ABC中,已知∠B,∠C均为一般锐角,∠B>∠C,AE是△ABC的角平分线,若P为线段AE上一个动点(P不与E重合),且PF⊥BC于点F时,请写出∠EPF与∠B,∠C的关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
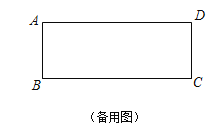
【题目】在矩形ABCD中,AB=4,BC=10,E是直线AD上任意一点(不与点A重合),点A关于直线BE的对称点为A′,AA′所在直线与直线BC交于点F.
(1)如图①,当点E在线段AD上时,①若△ABE ∽△DEC,求AE的长;
②设AE=x,BF=y,求y与x的函数表达式.
(2)线段DA′的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
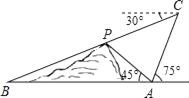
【题目】如图,在小山的东侧A庄,有一热气球,由于受西风的影响,以每分钟35米的速度沿着与水平方向成75度角的方向飞行,40分钟时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30度,又在A庄测得山顶P的仰角为45度,求A庄与B庄的距离___________,山高__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北方某水果商店从南方购进一种水果,其进货成本是每吨0.4万元,根据市场调查这种水果在北方市场上的销售量y(吨)与每吨的销售价x(万元)之间的函数关系如下图所示:
(1)求出销售量y与每吨销售价x之间的函数关系式;
(2)如果销售利润为w(万元),请写出w与x之间的函数关系式;
(3)当每吨销售价为多少万元时,销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角沿直线
的一个角沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
(1)求线段![]() 的长度;
的长度;
(2)求直线![]() 所对应的函数表达式;
所对应的函数表达式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 中,AB=15,AC=13,高 AD=12,则△ABC 的周长是( )
A. 42B. 32C. 42 或 32D. 42 或 37
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com