
【题目】△ABC 中,AB=15,AC=13,高 AD=12,则△ABC 的周长是( )
A. 42B. 32C. 42 或 32D. 42 或 37
【答案】C
【解析】
本题应分两种情况进行讨论:
(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;
(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出.
此题应分两种情况说明:
(1)当△ABC为锐角三角形时,在Rt△ABD中,
BD=![]() ,
,
在Rt△ACD中,
CD=![]()
∴BC=5+9=14
∴△ABC的周长为:15+13+14=42;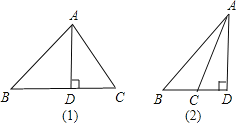
(2)当△ABC为钝角三角形时,
在Rt△ABD中,BD=9,
在Rt△ACD中,CD=5,
∴BC=9-5=4.
∴△ABC的周长为:15+13+4=32
∴当△ABC为锐角三角形时,△ABC的周长为42;当△ABC为钝角三角形时,△ABC的周长为32.
综上所述,△ABC的周长是42或32.
故选:C.


科目:初中数学 来源: 题型:
【题目】在解不等式|x+1|>2时,我们可以采用下面的解答方法:
①当x+1≥0时,|x+1|=x+1.
∴由原不等式得x+1>2.∴可得不等式组![]()
∴解得不等式组的解集为x>1.
②当x+1<0时,|x+1|=﹣(x+1).
∴由原不等式得﹣(x+1)>2.∴可得不等式组![]()
∴解得不等式组的解集为x<﹣3.
综上所述,原不等式的解集为x>1或x<﹣3.
请你仿照上述方法,尝试解不等式|x﹣2|≤1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我市某一天内的气温变化图,根据图象,下列说法中错误的是( )

A.这一天中最高气温是26℃
B.这一天中最高气温与最低气温的差为16℃
C.这一天中2时至14时之间的气温在逐渐升高
D.这一天中14时至24时之间的气温在逐渐降低
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲,乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示,根据图象信息回答下列问题:
(分钟)之间的函数关系如图所示,根据图象信息回答下列问题:

(1)图书馆与学校之间的距离为 米;
(2)当![]() 分钟时,甲乙两人相遇;
分钟时,甲乙两人相遇;
(3)乙的速度为 米/分钟;
(4)![]() 点的坐标为 .
点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承担了100米的道路改造工程任务,在确保工程质量的前提下,实际施工时每天改造道路比原计划多10米,结果提前5天完成了任务,求原计划平均每天改造道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为边
为边![]() 上一点,
上一点,![]() 为边
为边![]() 的中点,过点
的中点,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连结
,连结![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若点![]() 为边
为边![]() 的中点,当线段BC与线段AC满足什么数量关系时,四边形
的中点,当线段BC与线段AC满足什么数量关系时,四边形![]() 为正方形.
为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课上教师呈现一个问题

甲、乙、丙三位同学用不同的方法添加辅助线解决问题,如下图:
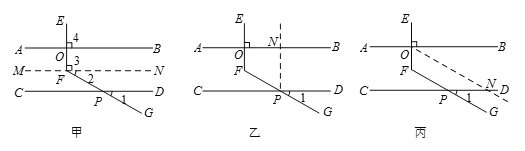
甲同学辅助线的做法和分析思路如下:

(1)请你根据乙同学所画的图形,描述辅助线的做法,并写出相应的分析思路.
辅助线:___________________;
分析思路:
(2)请你根据丙同学所画的图形,求∠EFG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73.
≈1.73.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学完二次根式一章后,小易同学看到这样一题:“函数![]() 中,自变量
中,自变量![]() 的取值范围是什么?”这个问题很简单,根据二次根式的性质很容易得到自变量
的取值范围是什么?”这个问题很简单,根据二次根式的性质很容易得到自变量![]() 的取值范围.联想到一次函数,小易想进一步研究这个函数的图象和性质.以下是他的研究步骤:
的取值范围.联想到一次函数,小易想进一步研究这个函数的图象和性质.以下是他的研究步骤:
第一步:函数![]() 中,自变量
中,自变量![]() 的取值范围是_____________.
的取值范围是_____________.
第二步:根据自变量取值范围列表:
| -1 | 0 | 1 | 2 | 3 | 4 | |
| 0 | 1 |
|
| 2 |
|
![]() __________.
__________.
第三步:描点画出函数图象.
在描点的时候,遇到了![]() ,
,![]() 这样的点,小易同学用所学勾股定理的知识,找到了画图方法,如图所示:
这样的点,小易同学用所学勾股定理的知识,找到了画图方法,如图所示:

你能否从中得到启发,在下面的![]() 轴上标出表示
轴上标出表示![]() 、
、![]() 、
、![]() 的点,并画出
的点,并画出![]() 的函数图象.
的函数图象.

第四步:分析函数的性质.
请写出你发现的函数的性质(至少写两条):
____________________________________________________________________________________________
____________________________________________________________________________________________
第五步:利用函数![]() 图象解含二次根式的方程和不等式.
图象解含二次根式的方程和不等式.
(1)请在上面坐标系中画出![]() 的图象,并估算方程
的图象,并估算方程![]() 的解.
的解.
(2)不等式![]() 的解是__________________.
的解是__________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com