
分析 先利用加减消元法解二元一次方程组,求得用a表示的x、y,根据方程组的解满足不等式x+y>3可得关于a的不等式,解不等式即可.
解答 解:$\left\{\begin{array}{l}{x+2y=3①}\\{2x+y=6a②}\end{array}\right.$
①-②×2,得:-3x=-12a-3,即x=4a-1,
将x=4a-1代入②,得:8a-2+y=6a,
解得:y=-2a+2,
∴方程组的解为$\left\{\begin{array}{l}{x=4a-1}\\{y=-2a+2}\end{array}\right.$,
∵方程组的解满足不等式x+y>3,
∴4a-1+(-2a+2)>3,
解得:a>1,
故答案为a>1.
点评 本题主要考查解二元一次方程组和一元一次不等式,熟练掌握解二元一次方程组的基本方法和解不等式的基本步骤是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在直角三角尺ABC中,∠C=90°,把直角三角尺ABC放置在圆上,AB经过圆心O,AC与⊙O相交于D,E两点,点C,D,E的刻度分别是0cm,2cm,5cm,BC与⊙O相切于F点,那么⊙O的半径是3.5cm.
如图,在直角三角尺ABC中,∠C=90°,把直角三角尺ABC放置在圆上,AB经过圆心O,AC与⊙O相交于D,E两点,点C,D,E的刻度分别是0cm,2cm,5cm,BC与⊙O相切于F点,那么⊙O的半径是3.5cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
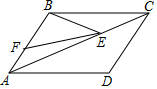 已知,如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E为AD上,BE=12cm,CE=5cm,则?ABCD的周长为39cm.
已知,如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E为AD上,BE=12cm,CE=5cm,则?ABCD的周长为39cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com