
【题目】如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP= ![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④ ![]() 为定值.其中一定成立的是 .
为定值.其中一定成立的是 .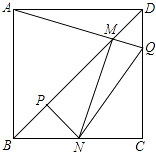
【答案】①②③④
【解析】解:如图1所示:
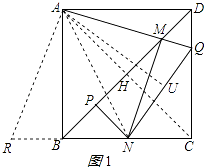
作AU⊥NQ于U,连接AN,AC,
∵∠AMN=∠ABC=90°,
∴A,B,N,M四点共圆,
∴∠NAM=∠DBC=45°,∠ANM=∠ABD=45°,
∴∠ANM=∠NAM=45°,
∴AM=MN,故①正确.
由同角的余角相等知,∠HAM=∠PMN,
在△AHM和△MPN中,
 ,
,
∴△AHM≌△MPN(AAS),
∴MP=AH= ![]() AC=
AC= ![]() BD,故②正确,
BD,故②正确,
∵∠BAN+∠QAD=∠NAQ=45°,
∴△ADQ绕点A顺时针旋转90度至△ABR,使AD和AB重合,连接AN,
则∠RAQ=90°,△ABR≌△ADQ,
∴AR=AQ,∠RAN=90°﹣45°=45°=∠NAM,
在△AQN和△ANR中,
 ,
,
∴△AQN≌△ANR(SAS),
∴NR=NQ,
则BN=NU,DQ=UQ,
∴点U在NQ上,有BN+DQ=QU+UN=NQ,故③正确.
如图2所示,作MS⊥AB,垂足为S,作MW⊥BC,垂足为W,点M是对角线BD上的点,
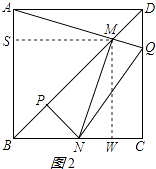
∴四边形SMWB是正方形,
∴MS=MW=BS=BW,∠SMW=90°,
∴∠AMS=∠NMW,
在△AMS和△NMW中,
 ,
,
∴△AMS≌△NMW(ASA),
∴AS=NW,
∴AB+BN=SB+BW=2BW,
∵BW:BM=1: ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,故④正确.
,故④正确.
所以答案是:①②③④.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.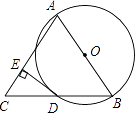
(1)求证:DE为⊙O的切线;
(2)若⊙O的半径为5,∠BAC=60°,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年5月14日川航3U863航班挡风玻璃在高空爆裂,机组临危不乱,果断应对,正确处置,顺利返航,避免了一场灾难的发生,创造了世界航空史上的奇迹!下表给出了距离地面高度与所在位置的温度之间的大致关系.根据下表,请回答以下几个问题:
距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
所在位置的温度(℃) | 20 | 14 | 8 | 2 |
|
(1)上表反映的两个变量中,______是自变量,______是因变量.
(2)若用h表示距离地面的高度,用y表示表示温度,则y与h的之间的关系式是:__________;
当距离地面高度5千米时,所在位置的温度为:_________℃.
如图是当日飞机下降过程中海拔高度与玻璃爆裂后立即返回地面所用时间关系图.根据图象回答以下问题:
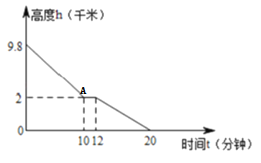
(3)点A表示的意义是什么?返回途中飞机在2千米高空水平大约盘旋了几分钟?
(4)飞机发生事故时所在高空的温度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
![]()
(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 和直线
和直线![]() 互相垂直,垂足为
互相垂直,垂足为![]() ,直线
,直线![]() 于点B,E是线段AB上一定点,D为线段OB上的一动点(点D不与点O、B重合),
于点B,E是线段AB上一定点,D为线段OB上的一动点(点D不与点O、B重合),![]() 直
直![]() 于点
于点![]() ,连接AC.
,连接AC.

(1)当![]() ,则
,则![]() ___________°;
___________°;
(2)当![]() 时,请判断CD与AC的位置关系,并说明理由;
时,请判断CD与AC的位置关系,并说明理由;
(3)若![]() 、
、![]() 的角平分线的交点为P,当点D在线段
的角平分线的交点为P,当点D在线段![]() 上运动时,问
上运动时,问![]() 的大小是否会发生变化?若不变,求出
的大小是否会发生变化?若不变,求出![]() 的大小,并说明理由;若变化,求其变化范围.
的大小,并说明理由;若变化,求其变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,于是
∠BAC=60°,于是![]() =
= ![]() =
=![]() ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;
②请直接写出线段AD,BD,CD之间的等量关系式;
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O为直线BC上一定点,点A在直线外一定点.在直线BC上取点P,使得以O、A、P为顶点的三角形为等腰三角形.
(1)当∠AOC=30°时,如果我们通过分类讨论、画图尝试可以找到满足条件的点P共有______个.
(2)若在直线BC上有且只有两个满足条件的点P,则∠AOC=______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com