
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,并交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D.
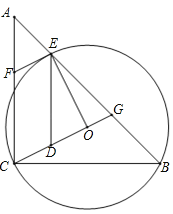
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,![]() =2,求BG的值.
=2,求BG的值.
【答案】(1)见解析;(2)BG=![]() .
.
【解析】
(1)先证明∠COE=2∠B=90°,根据EF是⊙O的切线,得到EF∥OC,又DE∥CF,可得到四边形CDEF是平行四边形;
(2)过G作GN⊥BC于N
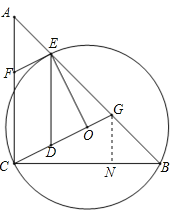
tan∠EDO=tan∠CGN=![]() =2,CN=2GN,CN+BN=2GN+GN=3,GN=1,得到
=2,CN=2GN,CN+BN=2GN+GN=3,GN=1,得到
BG=![]() GN=
GN=![]() .
.
(1)∵在△ABC中,AC=BC,∠ACB=90°,
∴∠B=45°,
∴∠COE=2∠B=90°,
∵EF是⊙O的切线,
∴∠FEO=90°,
∴EF∥OC,
∵DE∥CF,
∴四边形CDEF是平行四边形;
(2)过G作GN⊥BC于N.
∴△GNB是等腰直角三角形,
∴NB=GN,
∵四边形CDEF是平行四边形,
∴∠FCD=∠FED,
∵∠ACD+∠GCB=∠GCB+∠CGN=90°,
∴∠CGN=∠ACD,
∴∠CGN=∠DEF,
∵![]() =2,
=2,
∴tan∠EDO=tan∠CGN=![]() =2,
=2,
∴CN=2GN,
∴CN+BN=2GN+GN=3,
∴GN=1,
∴BG=![]() GN=
GN=![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,已知直线y=ax+b与双曲线y=![]() (x>0)交于A(x1,y1),B(x2,y2)两点,点A与点B不重合,直线AB与x轴交于点P(x0,0),与y轴交于点C.
(x>0)交于A(x1,y1),B(x2,y2)两点,点A与点B不重合,直线AB与x轴交于点P(x0,0),与y轴交于点C.
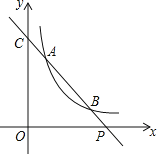
(1)若A、B两点坐标分别为(1,4),(4,y2),求点P的坐标;
(2)若b=y1+1,x0=6,且y1=2y2,求A,B两点的坐标;
(3)若将(1)中的点A,B绕原点O顺时针旋转90°,A点对应的点为A′,B点的对应点为B′点,连接AB′,A′B′,动点M从A点出发沿线段AB′以每秒1个单位长度的速度向终点B′运动;动点N同时从B′点出发沿线段B′A′以每秒1个单位长度的速度向终点A′运动,当其中一个点停止运动时另一个点也随之停止运动.设运动的时间为t秒,试探究:是否存在使△MNB′为等腰直角三角形的t值,若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB向点B移动(不与点A、B重合),一直到达点B为止;同时,点Q从点C出发沿CD向点D移动(不与点C、D重合).运动时间设为t秒.
(1)若点P、Q均以3cm/s的速度移动,则:AP= cm;QC= cm.(用含t的代数式表示)
(2)若点P为3cm/s的速度移动,点Q以2cm/s的速度移动,经过多长时间PD=PQ,使△DPQ为等腰三角形?
(3)若点P、Q均以3cm/s的速度移动,经过多长时间,四边形BPDQ为菱形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)求这个二次函数的表达式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的长方形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留根号)?

查看答案和解析>>
科目:初中数学 来源: 题型:
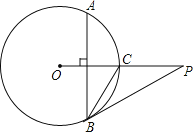
【题目】如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com