
【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28,∠AGF=80,FH平分∠EFG.
(1)说明:DC∥AB;
(2)求∠PFH的度数.
【答案】
(1)
∵ DC∥FP,
∴∠2=∠C.
∵ ∠1=∠2,
∴∠1=∠C,
∴DC∥AB.
(2)
∵ DC∥FP,DC∥AB,
∴∠PFE=∠FED=28,∠PFG=∠AGF=80,
∴∠EFG=∠PFE+∠PFG=28+80=108,
∵ FH平分∠EFG,
∴∠EFH=![]() ∠EFG=54,
∠EFG=54,
则∠PFH=∠EFH-∠PFE=54-28=26°.
【解析】(1)根据平行线的判定定理去判断;
(2)要求∠PFH,则要求∠EFH和∠PFE,根据平行线的性质可分别求出∠EFH和∠PFE.
【考点精析】通过灵活运用角的平分线和平行线的判定,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行即可以解答此题.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,A、B在一直线上,小明从点A出发沿AB方向匀速前进,4秒后走到点D,此时他(CD)在某一灯光下的影长为AD,继续沿AB方向以同样的速度匀速前进4秒后到点F,此时他(EF)的影长为2米,然后他再沿AB方向以同样的速度匀速前进2秒后达点H,此时他(GH)处于灯光正下方.
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明沿AB方向匀速前进的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90,点D为AB边上的一点,

(1)试说明:∠EAC=∠B ;
(2)若AD=15,BD=36,求DE的长.
(3)若点D在A、B之间移动,当点D为 时,AC与DE互相平分.
(直接写出答案,不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点在格点上.
(1)作出与△ABC关于x轴对称的图形△A1B1C1;
(2)求出A1,B1,C1三点坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
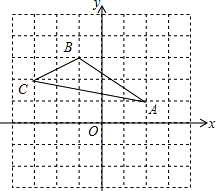
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(﹣1,3),C(﹣3,2).
(1)作出△ABC关于x轴对称的△A1B1C1;
(2)点A1的坐标 ,点B1的坐标 ;
(3)点P(a,a﹣2)与点Q关于x轴对称,若PQ=8,则点P的坐标 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com