
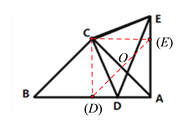
【题目】如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90,点D为AB边上的一点,

(1)试说明:∠EAC=∠B ;
(2)若AD=15,BD=36,求DE的长.
(3)若点D在A、B之间移动,当点D为 时,AC与DE互相平分.
(直接写出答案,不必说明理由)
【答案】(1)证明见解析(2)39 (3)AB的中点
【解析】试题分析:
(1)先由∠ACB=∠ECD=90可得∠ECA=∠DCB,再由“SAS”证△ECA≌△DCB可得结论;
(2)由△ECA≌△DCB可得:AE=BD=36,由∠EAC=∠B=45°可证∠DAE=90°,从而得到△ADE是直角三角形,再由勾股定理可求得DE的长;
(3)如图,若AC与DE互相平分,由∠DCE=90°,易得CO=AO=![]() DE=OD=OE,从而可得∠ODA=∠OAD=45°,并由此得到∠DOA=90°,再证△COD为等腰直角三角形,可得∠CDO=45°,这样∠CDA=∠CDO+∠ODA=90°,即CD⊥AB,∴点D是AB的中点.
DE=OD=OE,从而可得∠ODA=∠OAD=45°,并由此得到∠DOA=90°,再证△COD为等腰直角三角形,可得∠CDO=45°,这样∠CDA=∠CDO+∠ODA=90°,即CD⊥AB,∴点D是AB的中点.
试题解析:
(1)∵∠ACB=∠ECD=90°,
∴∠ACB-∠ACD =∠ECD-∠ACD,
∴∠ECA=∠DCB ,
∵△ACB和△ECD都是等腰三角形,
∴EC=DC,AC=BC,
∴△ACE≌△BCD,
∴∠EAC=∠B.
(2)∵△ACE≌△BCD,
∴AE=BD=36,
∵∠EAC=∠B=45 °,
∴∠EAD=∠EAC+∠CAD=90°,
∴在Rt△ADE中, ![]() ,
,
∴DE2=152+362 ,
∴DE=39.
(3)当点D为AB的中点时,AC与DE互相平分,理由如下:
∵AC=BC,D为AB中点,∠ACB=90°,
∴CD=![]() AB=AD,∠CDA=90°,
AB=AD,∠CDA=90°,
∴∠DCA=∠DAC=45°,
∵∠ECD=90°,
∴∠ECO=45°=∠DCA,
又∵CD=CE,
∴CO为△DCE的中线.
∵∠CDA=90°,∠CDE=45°,
∴∠ODA=45°=∠CDE,
又∵CD=AD,
∴DO为△ADC的中线.
∴AC和DE互相平分.



 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣10,点C在数轴上表示的数是16.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动. ![]()
(1)问运动多少时BC=8(单位长度)?
(2)当运动到BC=8(单位长度)时,点B在数轴上表示的数是;
(3)P是线段AB上一点,当B点运动到线段CD上时,是否存在关系式 ![]() =3,若存在,求线段PD的长;若不存在,请说明理由.
=3,若存在,求线段PD的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将直线y=2x﹣4向上平移5个单位后,所得直线的表达式是________.那么将直线y=2x﹣4沿x轴向右平移3个单位得到的直线方程是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量,如表所示:
用电量(度) | 120 | 140 | 160 | 180 | 200 |
户数 | 2 | 3 | 6 | 7 | 2 |
则这20户家庭该月用电量的众数和中位数分别是( )
A.180,160
B.160,180
C.160,160
D.180,180
查看答案和解析>>
科目:初中数学 来源: 题型:
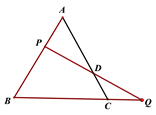
【题目】如图,△ABC中,∠A=60°,P为AB上一点, Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D, PD=DQ,证明:△ABC为等边三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com