
【题目】对于平面直角坐标系 xOy 中的点 A,给出如下定义:若存在点 B(不与点 A 重合,且直线 AB 不与 坐标轴平行或重合),过点 A 作直线 m∥x 轴,过点 B 作直线 n∥y 轴,直线 m,n 相交于点 C.当线段 AC,BC 的长度相等时,称点 B 为点 A 的等距点,称三角形 ABC 的面积为点 A 的等距面积. 例如:如 图,点 A(2,1),点 B(5,4),因为 AC= BC=3,所以 B 为点 A 的等距点,此时点 A 的等距面积为![]() .
.
(1)点 A 的坐标是(0,1),在点 B1(2,3),B2 (1, 1) , B3 (3, 2) 中,点A的等距点为 .
(2)点 A 的坐标是 (3,1) ,点 A 的等距点 B 在第三象限,
①若点 B 的坐标是 (5, 1) ,求此时点 A 的等距面积;
②若点 A 的等距面积不小于 2,请直接写出点 B 的横坐标 t 的取值范围.


【答案】(1)B1,B3;(2)①2;②t≤-5或-1≤t<0
【解析】
(1)根据等距点的定义可作判断;
(2)①计算等腰直角△ACB的面积即可;
②根据题意画出全等的等腰直角三角形ABC和AB1C1,发现点B可以在射线BF上或线段B1M上,可得t的取值.
解:(1)如图1,过A作x轴的平行线m,过B1作y轴的平行线n,交于C1,
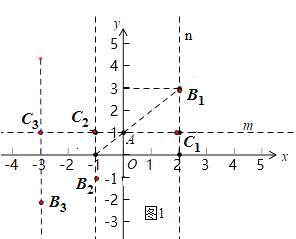
∵点A的坐标是(0,1),在点B1(2,3),
∴AC1=B1C1=2,即B1是点A的等距点,
同理:AC3=B3C3=3,B3是点A的等距点,
AC2≠B2C2,B2不是点A的等距点,
故答案为B1,B3;
(2)①如图2,根据题意,可知AC⊥BC.

∵A(-3,1),B(-5,-1),
∴AC=BC=2.
∴三角形ABC的面积为:![]() ACBC=
ACBC=![]() =2.
=2.
∴点A的等距面积为2.
②∵三角形ABC的面积为:![]() ACBC≥2,
ACBC≥2,
∴AC=BC≥2,
如图3,根据①作全等的等腰直角三角形ABC和AB1C1,发现点B可以在射线BF上或线段B1M上,
∵A(-3,1),
∴B(-5,-1),B1(-1,-1),
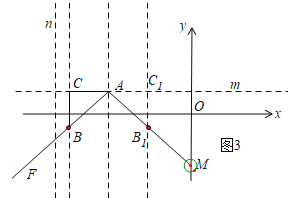
∴点B的横坐标t的取值范围是t≤-5或-1≤t<0.


科目:初中数学 来源: 题型:
【题目】某数码专营店销售甲、乙两种品牌智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4300 | 3600 |
售价(元/部) | 4800 | 4200 |
(1)该店销售记录显示.三月份销售甲、乙两种手机共17部,且销售甲种手机的利润恰好是销售乙种手机利润的2倍,求该店三月份售出甲种手机和乙种手机各多少部?
(2)根据市场调研,该店四月份计划购进这两种手机共20部,要求购进乙种手机数不超过甲种手机数的![]() ,而用于购买这两种手机的资金低于81500元,请通过计算设计所有可能的进货方案.
,而用于购买这两种手机的资金低于81500元,请通过计算设计所有可能的进货方案.
(3)在(2)的条件下,该店打算将四月份按计划购进的20部手机全部售出后,所获得利润的30%用于购买A,B两款教学仪器捐赠给某希望小学.已知购买A仪器每台300元,购买B仪器每台570元,且所捐的钱恰好用完,试问该店捐赠A,B两款仪器一共多少台?(直接写出所有可能的结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增加环保意识,某社区计划开展一次“减碳环保,减少用车时间”的宣传活动,对部分家庭五月份的平均每天用车时间进行了一次抽样调查,并根据收 集的数据绘制了如图所示的两幅不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)本次抽样调查了多少个家庭?
(2)将图①中的频数分布直方图补充完整;
(3)求用车时间在 1 小时~1.5 小时的部分对应的扇 形圆心角的度数;
(4)若该社区有车家庭有 1 600 个,请你估计该社区用车时间不超过 1.5 小时的约有多少个家庭.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有点 A(a﹣1,3),B(a+2,2a﹣1)
(1)若线段AB∥x轴,求点A、B的坐标;
(2)当点B到x轴的距离是点A到y轴的距离2倍时,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交OG于点H.
(1)求证:∠DAE=∠DCG.
(2)求线段HE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
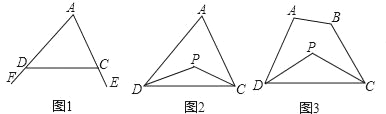
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
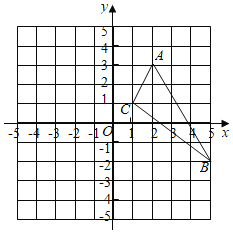
【题目】已知如图,在![]() 中,三个顶点的坐标分别为
中,三个顶点的坐标分别为![]() ,将
,将![]() 沿
沿 ![]() 轴负方向平移
轴负方向平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向平移
轴负方向平移![]() 个单位长度,得到
个单位长度,得到![]() ,其 中点
,其 中点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]()
![]() 直接写出平移后的
直接写出平移后的![]() 的顶点坐标:
的顶点坐标:
![]()
![]()
![]()
![]() 在坐标系中画出平移后的
在坐标系中画出平移后的![]()
![]() 求出
求出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,CD⊥AB,EF⊥AB,垂足分别为D、F.
(1)若∠1=∠2,试说明DG∥BC.
(2)若CD 平分∠ACB,∠A=60°,求∠B的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com