
分析 将几个代数式进行整理得出:①4β+1=22β+2,②$\frac{2}{{4}^{α}}$=21-2α,再比较即可.
解答 解:(1)因为:①4β+1=22β+2,②$\frac{2}{{4}^{α}}$=21-2α,k=2n且α,β,n为整数,
所以k=2n不能等于0,也不能等于-2,
所以①、②、③、④这4个代数式中与k相等的可能性只能是①和②;
(2)不能,理由如下:
因为:①4β+1=22β+2,②$\frac{2}{{4}^{α}}$=21-2α,
若代数式相等时,则有2β+2=1-2α,
可得2(α+β)=-1,
所以当α,β为整数,其2倍不能是-1,
所以4β+1与$\frac{2}{{4}^{α}}$两个代数式不能相等.
点评 此题考查同底数幂的除法,关键是把代数式整理为同底数.


科目:初中数学 来源: 题型:选择题
 如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若AB=m,CD=n,则△ABD的面积等于( )
如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若AB=m,CD=n,则△ABD的面积等于( )| A. | mn | B. | $\frac{1}{2}mn$ | C. | 2mn | D. | $\frac{1}{3}mn$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
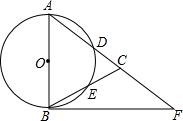 如图,在△ABC,AB=AC,以AB为直径的圆O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF.
如图,在△ABC,AB=AC,以AB为直径的圆O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
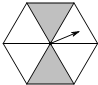 如图,一个正六边形转盘被分成6个全等三角形,任意转动这个转盘1次,当转盘停止时,指针指向阴影区域的概率是( )
如图,一个正六边形转盘被分成6个全等三角形,任意转动这个转盘1次,当转盘停止时,指针指向阴影区域的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com