
分析 (1)两边加上一次项系数一半的平方,左边配成完全平方的形式,再用直接开平方求出方程的根.
(2)先分解因式,即可得出两个一元一次方程,求出方程的解即可.
(3)求出b2-4ac的值,即可判断原方程无解;
(4)先分解因式,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)x2+4x=10;
x2+4x+4=14
(x+2)2=14
x+2=±$\sqrt{14}$
x=-2±$\sqrt{14}$
∴x1=-2+$\sqrt{14}$,x2=-2-$\sqrt{14}$;
(2)3x2+8x-3=0;
(3x-1)(x+3)=0,
3x-1=0,x+3=0,
x1=$\frac{1}{3}$,x2=-3;
(3)x2-2x+3=0;
b2-4ac=(-2)2-4×1×3=-8<0,
所以此方程在实数范围内无解.
(4)(x-2)(x-3)=12.
整理得,x2-5x-6=0,
(x-6)(x+1)=0,
∴x-6=0,x+1=0,
解得x1=6,x2=-1;
点评 本题考查了解一元一次方程和解一元二次方程的应用,解此题的关键是能选择适当的方法解一元二次方程.


科目:初中数学 来源: 题型:解答题
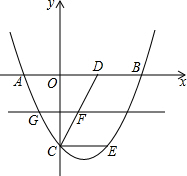 如图,抛物线y=$\frac{1}{2}$x2-x-4过平行四边形CEBD的三点,过DC中点F作直线m平行x轴,交抛物线左侧于点G.
如图,抛物线y=$\frac{1}{2}$x2-x-4过平行四边形CEBD的三点,过DC中点F作直线m平行x轴,交抛物线左侧于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
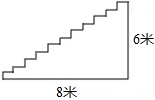 如图,凯瑞酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮老板算下,购买地毯多少钱?
如图,凯瑞酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮老板算下,购买地毯多少钱?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
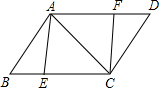 如图,已知点E、F分别是平行四边形ABCD的边BC、AD上的点,且BE=DF
如图,已知点E、F分别是平行四边形ABCD的边BC、AD上的点,且BE=DF查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com