
分析 从x>0,和x<0的角度分别求出二次函数,用求根公式,表示出当函数值为0时,x的值,相加即可.
解答 解:当x>0时,二次函数的解析式为:y=x2-2009x+2011,
当y=0时,x2-2009x+2011=0,
由求根公式,得:${x}_{1}=\frac{2009+\sqrt{(-2009)^{2}-4×2011}}{2}$,${x}_{2}=\frac{2009-\sqrt{(-2009)^{2}-4×2011}}{2}$,
∴x1+x2=2009,
当x<0时,二次函数的解析式为:y=x2+2009x+2011,
当y=0时,x2+2009x+2011=0,
由求根公式,得:${x}_{1}=\frac{-2009+\sqrt{200{9}^{2}-4×2011}}{2}$,${x}_{2}=\frac{-2009-\sqrt{200{9}^{2}-4×2011}}{2}$,
∴x1+x2=-2009,
∴横坐标的和为2009+(-2009)=0.
故答案为:0.
点评 本题主要考查二次函数与x轴的交点,解决此题的关键是从x>0和x<0两个角度求解.


科目:初中数学 来源: 题型:填空题
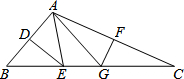 在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.若∠BAC=106°,则∠EAG=32°.
在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.若∠BAC=106°,则∠EAG=32°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
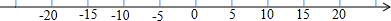
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1≤y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
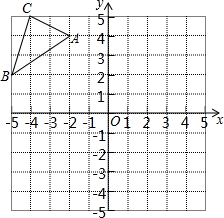 已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).
已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
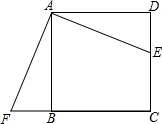 如图,点E在正方形ABCD的边CD上,把△ADE绕点A顺时针旋转90°至△ABF位置,如果AB=$\sqrt{3}$,∠EAD=30°,那么点E与点F之间的距离等于$2\sqrt{2}$.
如图,点E在正方形ABCD的边CD上,把△ADE绕点A顺时针旋转90°至△ABF位置,如果AB=$\sqrt{3}$,∠EAD=30°,那么点E与点F之间的距离等于$2\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com