
【题目】如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°. 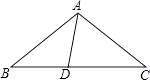
(1)求∠DAC的度数;
(2)求证:DC=AB.
【答案】
(1)解:∵AB=AC,
∴∠B=∠C=30°,
∵∠C+∠BAC+∠B=180°,
∴∠BAC=180°﹣30°﹣30°=120°,
∵∠DAB=45°,
∴∠DAC=∠BAC﹣∠DAB=120°﹣45°=75°
(2)证明:∵∠DAB=45°,
∴∠ADC=∠B+∠DAB=75°,
∴∠DAC=∠ADC,
∴DC=AC,
∴DC=AB
【解析】(1)由AB=AC,根据等腰三角形的两底角相等得到∠B=∠C=30°,再根据三角形的内角和定理可计算出∠BAC=120°,而∠DAB=45°,则∠DAC=∠BAC﹣∠DAB=120°﹣45°;(2)根据三角形外角性质得到∠ADC=∠B+∠DAB=75°,而由(1)得到∠DAC=75°,再根据等腰三角形的判定可得DC=AC,这样即可得到结论.
【考点精析】关于本题考查的等腰三角形的性质,需要了解等腰三角形的两个底角相等(简称:等边对等角)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
猜想结论:(要求用文字语言叙述) 写出证明过程(先画出图形,写出已知、求证).
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?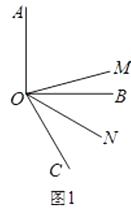
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;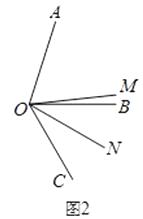
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.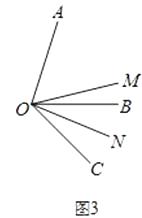
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表

我们把某格中字母和所得的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
(1)第3格的“特征多项式”为 ,第4格的“特征多项式”为 ,第n格的“特征多项式”为 ;
(2)若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16,求x,y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D. 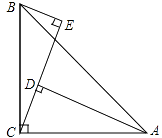
(1)求证:△ADC≌△CEB.
(2)AD=6cm,DE=4cm,求BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①直径是弦;②垂直于半径的直线是这个圆的切线;③圆只有一个外切三角形;④三点确定一个圆,其中假命题的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数y=﹣2x+1,下列结论正确的是( )
A. 图象经过点(﹣2,1) B. y随x的增大而增大
C. 图象不经过第三象限 D. 图象不经过第二象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com