
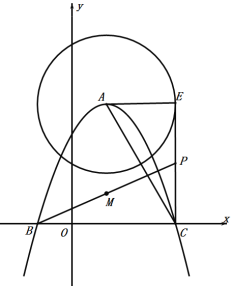
【题目】如图1,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 为抛物线的顶点,
为抛物线的顶点,![]() 为线段
为线段![]() 中点.
中点.
(1)求![]() 的值;
的值;
(2)求证:![]() ;
;
(3)以抛物线的顶点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,点
,点![]() 是圆上一动点,点
是圆上一动点,点![]() 为
为![]() 的中点(如图2);
的中点(如图2);
①当![]() 面积最大时,求
面积最大时,求![]() 的长度;
的长度;
②若点![]() 为
为![]() 的中点,求点
的中点,求点![]() 运动的路径长.
运动的路径长.
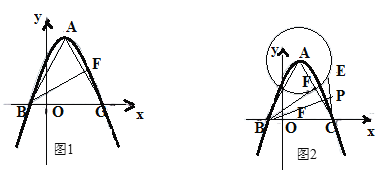
【答案】(1)![]() ,
,![]() ;(2)证明见解析;(3)①
;(2)证明见解析;(3)①![]() 或
或![]() ;②
;②![]() .
.
【解析】
(1)将![]() 代入二次函数的解析式
代入二次函数的解析式![]() 即可求解;
即可求解;
(2)证得![]() 是等边三角形即可证得结论;
是等边三角形即可证得结论;
(3)①根据题意,当![]() 或
或![]() 时,
时,![]() 或
或![]() 面积最大,利用三角形中位线定理可求得
面积最大,利用三角形中位线定理可求得![]() 的长,利用勾股定理可求得
的长,利用勾股定理可求得![]() ,即可求得答案;
,即可求得答案;
②根据点M的运动轨迹是半径为2的![]() ,则
,则![]() 的中点
的中点![]() 的运动轨迹也是圆,同样,
的运动轨迹也是圆,同样,![]() 的中点
的中点![]() 的运动轨迹也是圆,据此即可求得答案.
的运动轨迹也是圆,据此即可求得答案.
∵二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,
两点,
∴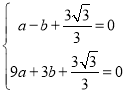 ,
,
解得: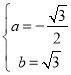 ,
,
故答案为:![]() ,
,![]() ;
;
(2)由(1)得:抛物线的解析式为![]() ,
,
∵二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,
两点,
∴抛物线的对称轴为:![]() ,
,
∴顶点![]() 的坐标为:
的坐标为:![]() ,
,![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∵![]() 为线段
为线段![]() 中点,
中点,
∴![]() ;
;
(3)①∵![]() 为定值,当
为定值,当![]() 时,
时,![]() 面积最大,如图,
面积最大,如图,
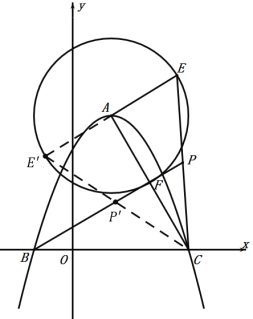
由(2)得![]() ,
,![]() ,
,![]() ,
,
∴![]() ∥
∥![]() ,
,
∵点![]() 为线段
为线段![]() 中点,点
中点,点![]() 为
为![]() 的中点,
的中点,
∴![]() ∥
∥![]() ,
,![]() ,
,
∴![]() 三点共线,
三点共线,
在Rt![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
同理,当![]() 时,
时,![]() 面积最大,
面积最大,
同理可求得:![]() ;
;
故答案为:![]() 或
或![]() ;
;
②如图,
∵点E的运动轨迹是![]() ,半径为
,半径为![]() ,
,
∴![]() 的中点
的中点![]() 的运动轨迹也是圆,半径为1,
的运动轨迹也是圆,半径为1,
∴![]() 的中点M的运动轨迹也是圆,半径为
的中点M的运动轨迹也是圆,半径为![]() ,
,
∴点M运动的路径长为:![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了扎实推进精准扶贫工作,某地出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种4种和5种帮扶措施的贫困户分别称为![]() 、
、![]() 、
、![]() 、
、![]() 类贫困户,为检查帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
类贫困户,为检查帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
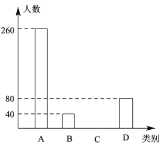

请根据图中信息回答下面的问题:
(1)本次抽样调查了 户贫困户;
(2)本次共抽查了 户![]() 类贫困户,请补全条形统计图;
类贫困户,请补全条形统计图;
(3)若该地共有13000户贫困户,请估计至少得到4项帮扶措施的大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是小区常见的漫步机,从侧面看如图2,踏板静止时,踏板连杆与立柱![]() 上的线段
上的线段![]() 重合,
重合,![]() 长为0.2米,当踏板连杆绕着点
长为0.2米,当踏板连杆绕着点![]() 旋转到
旋转到![]() 处时,测得
处时,测得![]() ,此时点
,此时点![]() 距离地面的高度
距离地面的高度![]() 为0.44米.求:
为0.44米.求:

(1)踏板连杆![]() 的长.
的长.
(2)此时点![]() 到立柱
到立柱![]() 的距离.(参考数据:
的距离.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,可计算出甲的平均成绩是 环(直接写出结果);
(2)已知乙的平均成绩是9环,试计算其第二次测试成绩的环数;
(3)分别计算甲、乙六次测试成绩的方差,根据计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]()
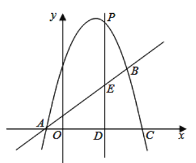
(1)求抛物线的解析式.
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 点
点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当
.当![]() 时,求
时,求![]() 点坐标;
点坐标;
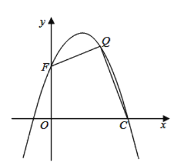
(3)如图所示,设抛物线与![]() 轴交于点
轴交于点![]() ,在抛物线的第一象限内,是否存在一点
,在抛物线的第一象限内,是否存在一点![]() ,使得四边形
,使得四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 箱中装有3张相同的卡片,它们分别写有数字1,2,4;
箱中装有3张相同的卡片,它们分别写有数字1,2,4;![]() 箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从
箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从![]() 箱、
箱、![]() 箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
(1)两张卡片上的数字恰好相同的概率.
(2)如果取出![]() 箱中卡片上的数字作为十位上的数字,取出
箱中卡片上的数字作为十位上的数字,取出![]() 箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
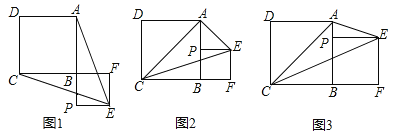
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
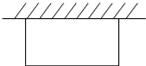
【题目】某农场要建一个长方形的养鸡场,鸡场的一边靠墙,(墙长25m)另外三边用木栏围成,木栏长40m.
(1)若养鸡场面积为200m2,求鸡场靠墙的一边长.
(2)养鸡场面积能达到250m2吗?如果能,请给出设计方案;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com