
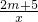 的图象的两个分支在各自的象限内y随x的增大而减小.求满足上述条件的m的整数值.
的图象的两个分支在各自的象限内y随x的增大而减小.求满足上述条件的m的整数值.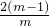 ,ab=
,ab=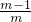 ,
,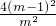 -
-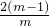 ,
,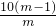 -
-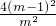 +
+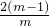 >8,
>8,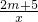 的图象的两个分支在各自的象限内y随x的增大而减小,
的图象的两个分支在各自的象限内y随x的增大而减小, ,
, <m<-1,
<m<-1,

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com