
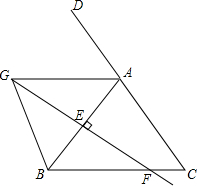
 已知,如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB、BC于E、F,∠BAD的平分线交直线EF于G,求证:BG=BF.
已知,如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB、BC于E、F,∠BAD的平分线交直线EF于G,求证:BG=BF. 分析 根据等腰三角形的性质得到∠ABC=∠ACB,由外角的性质得到∠DAB=∠ABC+∠ACB,根据角平分线的定义得到∠DAG=∠BAG,等量代换得到∠GAD=∠C,根据平行线的判定得到AG∥BC,由平行线的性质得到∠GAB=∠ABC,根据垂直平分线的性质得到AG=BG,即可得到结论.
解答 证明:∵AB=AC,
∴∠ABC=∠ACB,
∵∠DAB=∠ABC+∠ACB,
∵AG平分∠DAB,
∴∠DAG=∠BAG,
∴∠GAD=∠C,
∴AG∥BC,
∴∠GAB=∠ABC,
∵AB的垂直平分线分别交AB、BC于E、F,
∴AG=BG,
∴∠GBA=∠GAB,
∴∠GBE=∠FBE,
∵BE⊥GF,
∴BG=BF.
点评 本题考查了等腰三角形的判定和性质,线段垂直平分线的性质,角平分线的定义,平行线的判定和性质,熟练正确各定理是解题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:填空题
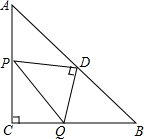 如图,等腰Rt△ABC中,∠C=90°,AC=BC,D是AB的中点,P是线段AC上的动点,连接PD,作DQ⊥PD交线段CB于Q,连接PQ,则点P从A向C方向运动过程中,△CPQ的面积变化是先逐渐增大,再逐渐减小.
如图,等腰Rt△ABC中,∠C=90°,AC=BC,D是AB的中点,P是线段AC上的动点,连接PD,作DQ⊥PD交线段CB于Q,连接PQ,则点P从A向C方向运动过程中,△CPQ的面积变化是先逐渐增大,再逐渐减小.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com