
(8分)已知:如图,AB是⊙O的直径,C、D为⊙O上两点,CF⊥AB于点F,CE⊥AD的延长线于点E,且 CE=CF.

(1)求证:CE是⊙O的切线;
(2)若AD=CD=6,求四边形ABCD的面积.
(1)证明见试题解析;(2) .
.
【解析】
试题分析:(1)连接OC.根据角平分线性质定理的逆定理,得∠CAE=∠CAB.根据OC=OA,得到∠CAB=∠OCA,从而得到∠CAE=∠OCA,根据内错角相等,两条直线平行,得到OC∥AE,从而根据切线的判定证明结论;
(2)根据AD=CD,得到∠DAC=∠DCA=∠CAB,从而DC∥AB,得到四边形AOCD是平行四边形.根据平行四边形的性质,得OC=AD=6,则AB=12.根据∠CAE=∠CAB,得到弧CD=弧CB,则△OCB是等边三角形,根据等边三角形的性质求得CF=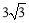 ,再根据梯形的面积公式进行计算.
,再根据梯形的面积公式进行计算.
试题解析:(1)连接OC.
∵CF⊥AB,CE⊥AD,且CE=CF,∴∠CAE=∠CAB.
∵OC=OA,∴∠CAB=∠OCA,∴∠CAE=∠OCA,∴OC∥AE,∴OC⊥CE,
又∵OC是⊙O的半径,∴CE是⊙O的切线;
(2)∵AD=CD,∴∠DAC=∠DCA=∠CAB,∴DC∥AB.
∵∠CAE=∠OCA,∴OC∥AD,∴四边形AOCD是平行四边形.∴OC=AD=6,AB=12.
∵∠CAE=∠CAB,∴弧CD=弧CB,∴CD=CB=6,∴△OCB是等边三角形,∴CF=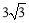 ,
,
∴S四边形ABCD=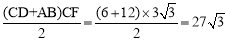 .
.

考点:1.切线的判定与性质;2.圆周角定理.
考点分析: 考点1:圆 圆,圆的有关性质与圆的有关计算是近几年各地中考命题的重点内容。题型以填空题,选择题和解答题为主,也有以阅读理解,条件开放,结论开放探索题作为新的题型,分值一般是6-12分,难易度为中,考察内容:①圆的有关性质的应用。垂径定理是重点。② 直线和圆,圆和圆的位置关系的判定及应用。③弧长,扇形面积,圆柱,圆锥的侧面积和全面积的计算④圆与相似三角形,三角函数的综合运用以及有关的开放题,探索题。突破方法:①熟练掌握圆的有关行政,掌握求线段,角的方法,理解概念之间的相互联系和知识之间的相互转化。②理解直线和原的三种位置关系,掌握切线的性质和判定的歌,会根据条件解决圆中的动态问题。③掌握有两圆半径的和或差与圆心距的大小关系来盘底的那个两个圆的位置关系,对中考试题中常出现的阅读理解题,探索题,要灵活运用圆的有关性质,进行合理推理与计算。④掌握弧长,扇形面积计算公式。⑤理解圆柱,圆锥的侧面展开图⑥对组合图形 的计算要灵活运用计算方法解题。 试题属性

科目:初中数学 来源:2014-2015学年福建省武夷山市九年级上学期期末质量监测数学试卷(解析版) 题型:解答题
(8分)如图1,正方形ABCD是一个6×6网格电子屏的示意图,其中每个小正方形的边长为1.位于AD中点处的光点P按图-2的程序移动.
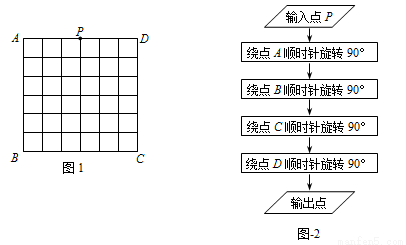
(1)请在图-1中画出光点P经过的路径;
(2)求光点P经过的路径总长(结果保留π).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省九年级上学期第一次月考数学试卷(解析版) 题型:填空题
方程(x+5)(x-7)=-26,化成一般形式是 ,其二次项的系数和一次项系数的和是 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年天津市九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图所示,长为4 ,宽为3
,宽为3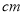 的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板上点A位置变化为
的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板上点A位置变化为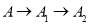 ,由
,由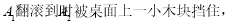 此时长方形木板的边
此时长方形木板的边 与桌面成30°角,则点A翻滚到A2位置时所经过的路径总长度为 cm.
与桌面成30°角,则点A翻滚到A2位置时所经过的路径总长度为 cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com