
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
![]() 若
若![]() ,则
,则![]() 的度数为______;
的度数为______;
![]() 若
若![]() ,求
,求![]() 的度数;
的度数;
![]() 猜想
猜想![]() 与
与![]() 之间存在什么数量关系?并说明理由;
之间存在什么数量关系?并说明理由;
![]() 当
当![]() 且点E在直线AC的上方时,这两块三角尺是否存在AD与BC平行的情况?若存在,请直接写出
且点E在直线AC的上方时,这两块三角尺是否存在AD与BC平行的情况?若存在,请直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)猜想:
;(3)猜想:![]() ,理由见解析;(4)存在,
,理由见解析;(4)存在,![]()
【解析】分析:(1)根据∠DCE和∠ACD的度数,求得∠ACE的度数,再根据∠BCE求得∠ACB的度数;
(2)根据∠BCE和∠ACB的度数,求得∠ACE的度数,再根据∠ACD求得∠DCE的度数;
(3)根据∠ACE=90°-∠DCE以及∠ACB=∠ACE+90°,进行计算即可得出结论;
(4)分三种情况进行讨论:当CB∥AD时,当EB∥AC时,当BE∥AD时,分别求得∠ACE角度.
详解:![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;
![]() 猜想:
猜想:![]()
理由如下:![]()
又![]()
![]()
即![]() ;
;
(4)15°、30°、45°;
理由:当CB∥AD时,∠ACE=30°;
当EB∥AC时,∠ACE=45°;
当BE∥AD时,∠ACE=15°.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC的外角∠ACD的平分线CP与∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP的度数是( )
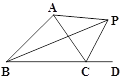
A. 30°; B. 40°; C. 50°; D. 60°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,任意两点A (x1,y1),B (x2,y2)规定运算:①A![]() B=( x1+ x2, y1+ y2);②A
B=( x1+ x2, y1+ y2);②A![]() B= x1 x2+y1 y2③当x1= x2且y1= y2时A=B有下列四个命题:
B= x1 x2+y1 y2③当x1= x2且y1= y2时A=B有下列四个命题:
(1)若A(1,2),B(2,–1),则A![]() B=(3,1),A
B=(3,1),A![]() B=0;
B=0;
(2)若A![]() B=B
B=B![]() C,则A=C;(3)若A
C,则A=C;(3)若A![]() B=B
B=B![]() C,则A=C;
C,则A=C;
(4)对任意点A、B、C,均有(A![]() B )
B ) ![]() C=A
C=A![]() ( B
( B![]() C )成立.其中正确命题的个数为( )
C )成立.其中正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你会求(a﹣1)(a2014+a2013+a2012+…+a2+a+1)的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
![]() ;
;
![]() ;
;
![]() .
.
(1)由上面的规律我们可以大胆猜想,得到(a﹣1)(a2014+a2013+a2012+…+a2+a+1)=________
利用上面的结论,求:
(2)22014+22013+22012+…+22+2+1的值是 。
(3)求52014+52013+52012+…+52+5+1的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对三种国庆活动方案的意见,对该校学生进行了一次抽样调查(被调查学生至多赞成其中的一种方案),现将调查结果绘制成如图两幅不完整的统计图. 
请根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了名学生;扇形统计图中方案1所对应的圆心角的度数为度;
(2)请把条形统计图补充完整;
(3)已知该校有1000名学生,试估计该校赞成方案1的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援某灾区,某市民政局组织募捐了240吨救灾物资,现租用甲、乙两种货车,将这批救灾物资一次性全部运往灾区,它们的载货量和租金如下表:
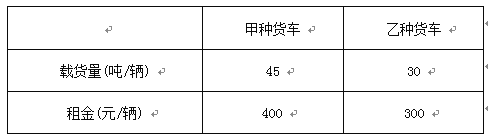
如果计划租用6辆货车,且租车的总费用不超过2 300元,求最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据提示填空(8分)
如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.

因为EF∥AD
所以∠2=____(____________________________)
又因为∠1=∠2
所以∠1=∠3(______________)
所以AB∥_____(_____________________________)
所以∠BAC+______=180°(_____________________)
因为∠BAC=80° 所以∠AGD=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC的各边都延长一倍至A′、B′、C′,连接这些点,得到一个新的三角形△A′B′C′,若△ABC的面积为1,则△A′B′C′的面积是( )

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com