
【题目】如图,Rt△ACB中,∠ACB=90°,∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD﹣AH=AB;④DG=AP+GH.其中正确的是( )

A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
①根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠CAP,再根据角平分线的定义∠ABP=![]() ∠ABC,然后利用三角形的内角和定理整理即可得解;
∠ABC,然后利用三角形的内角和定理整理即可得解;
②先求出∠APB=∠FPB,再利用“角边角”证明△ABP和△FBP全等,根据全等三角形对应边相等得到AB=BF,AP=PF;
③根据直角的关系求出∠AHP=∠FDP,然后利用“角角边”证明△AHP与△FDP全等,根据全等三角形对应边相等可得DF=AH;
④根据PF⊥AD,∠ACB=90°,可得AG⊥DH,然后求出∠ADG=∠DAG=45°,再根据等角对等边可得DG=AG,再根据等腰直角三角形两腰相等可得GH=GF,然后求出DG=GH+AF,有直角三角形斜边大于直角边,AF>AP,从而得出本小题错误.
解:①∵∠ABC的角平分线BE和∠BAC的外角平分线,
∴∠ABP=![]() ∠ABC,
∠ABC,
∠CAP=![]() (90°+∠ABC)=45°+
(90°+∠ABC)=45°+![]() ∠ABC,
∠ABC,
在△ABP中,∠APB=180°-∠BAP-∠ABP,
=180°-(45°+![]() ∠ABC+90°-∠ABC)-
∠ABC+90°-∠ABC)-![]() ∠ABC,
∠ABC,
=180°-45°- ![]() ∠ABC-90°+∠ABC-
∠ABC-90°+∠ABC-![]() ∠ABC,
∠ABC,
=45°,故本小题正确;
②∵PF⊥AD,∠APB=45°(已证),
∴∠APB=∠FPB=45°,
∵∵PB为∠ABC的角平分线,
∴∠ABP=∠FBP,
在△ABP和△FBP中,
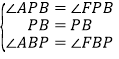 ,
,
∴△ABP≌△FBP(ASA),
∴AB=BF,AP=PF;故②正确;
③∵∠ACB=90°,PF⊥AD,
∴∠FDP+∠HAP=90°,∠AHP+∠HAP=90°,
∴∠AHP=∠FDP,
∵PF⊥AD,
∴∠APH=∠FPD=90°,
在△AHP与△FDP中,
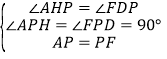
∴△AHP≌△FDP(AAS),
∴DF=AH,
∵BD=DF+BF,
∴BD=AH+AB,
∴BD-AH=AB,故③小题正确;
④∵PF⊥AD,∠ACB=90°,
∴AG⊥DH,
∵AP=PF,PF⊥AD,
∴∠PAF=45°,
∴∠ADG=∠DAG=45°,
∴DG=AG,
∵∠PAF=45°,AG⊥DH,
∴△ADG与△FGH都是等腰直角三角形,
∴DG=AG,GH=GF,
∴DG=GH+AF,
∵AF>AP,
∴DG=AP+GH不成立,故本小题错误,
综上所述①②③正确.
故选:C.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:
学习了无理数后,小航用这样的方法估算![]() 的近似值:
的近似值:
由于![]() ,不妨设
,不妨设![]() (
(![]() ),
),
所以![]() ,可得
,可得![]() .
.
由![]() 可知
可知![]() ,所以
,所以![]() ,
,
解得![]() , 则
, 则![]() .
.
依照小航的方法解决下列问题:
(1)估算![]() 的值.
的值.
(2)已知非负整数![]() 、
、![]() 、
、![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() .(用含
.(用含![]() 、
、![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点. 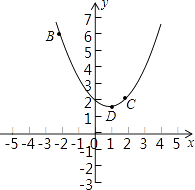
(1)试求抛物线的解析式;
(2)记抛物线顶点为D,求△BCD的面积;
(3)若直线y=﹣ ![]() x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上). 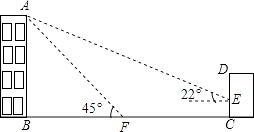
(参考数据:sin22°≈ ![]() ,cos22°
,cos22° ![]() ,tan22
,tan22 ![]() )
)
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( ) 
A.点(0,3)
B.点(2,3)
C.点(5,1)
D.点(6,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE,动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为__________秒时.△ABP和△DCE全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红家有一块L形的菜地,要把L形的菜地按如图所示分成两块面积相等的梯形,种上不同的蔬菜.这两个梯形的上底都是a m,下底都是b m,高都是(b-a) m.
(1)求小红家这块L形菜地的面积.(用含a、b的代数式表示)
(2)若a2+b2=15,ab=5,求小红家这块L形菜地的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
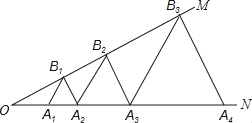
【题目】如图,∠MON=30°,点B1、B2、B3…和A1、A2、A3…分别在OM和ON上,且△A1B1A2、△A2B2A3、△A3B3A4、…分别为等边三角形,已知OA1=1,则△A2018B2018A2019的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(10,0)、C(0,3),直线 ![]() 与BC相交于点D,抛物线y=ax2+bx经过A、D两点.
与BC相交于点D,抛物线y=ax2+bx经过A、D两点.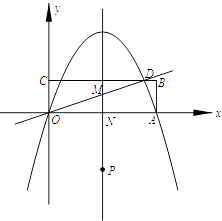
(1)求抛物线的解析式;
(2)连接AD,试判断△OAD的形状,并说明理由.
(3)若点P是抛物线的对称轴上的一个动点,对称轴与OD、x轴分别交于点M、N,问:是否存在点P,使得以点P、O、M为顶点的三角形与△OAD相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com