
����Ŀ������OABC��ֱ������ϵ�е�λ����ͼ��ʾ��A��C���������ֱ�ΪA��10��0����C��0��3����ֱ�� ![]() ��BC�ཻ�ڵ�D��������y=ax2+bx����A��D���㣮
��BC�ཻ�ڵ�D��������y=ax2+bx����A��D���㣮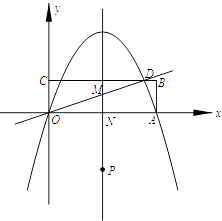
��1���������ߵĽ���ʽ��
��2������AD�����жϡ�OAD����״����˵�����ɣ�
��3������P�������ߵĶԳ����ϵ�һ�����㣬�Գ�����OD��x��ֱ��ڵ�M��N���ʣ��Ƿ���ڵ�P��ʹ���Ե�P��O��MΪ��������������OAD���ƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺������ã���D��������Ϊ3��
�ߵ�D��ֱ��y= ![]() x�ϣ�
x�ϣ�
���D��������9��3����
����D��9��3������A��10��0�����������߿ɵã� ![]() ��
��
��ã�  ��
��
�������ߵĽ���ʽΪ��y=�� ![]() x2+
x2+ ![]() x��
x��
��2��
�⣺�ߵ�D����Ϊ��9��3������A����Ϊ��10��0����
��OA=10��OD= ![]() =3
=3 ![]() ��AD=
��AD= ![]() =
= ![]() ��
��
�Ӷ��ɵ�OA2=OD2+AD2��
�ʿ��жϡ�OAD��ֱ�������Σ�
��3��
�⣺����ͼ�οɵõ���P�͵�N�غ�ʱ�������OPM�ס�ODA��
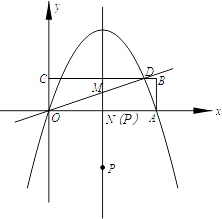
��ʱ��POM=��DOA����OPM=��ODA��
�ʿɵá�OPM�ס�ODA��OP= ![]() OA=5��
OA=5��
���ɵô�ʱ��P������Ϊ��5��0����
�ڹ���O��OD�Ĵ��߽��Գ����ڵ�P�䣬��ʱҲ�������P��OM�ס�ODA��
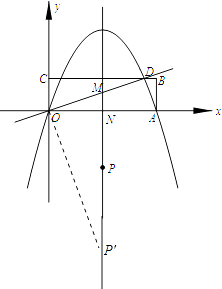
������ɵã���M�ĺ�����Ϊ5������ֱ�߷��̿ɵõ�M��������Ϊ ![]() ��
��
�ʿ����OM= ![]() ��
��
�ߡ�OP��M+��OMN=��DOA+��OMN=90�㣬
���OP��M=��DOA��
���P��OM�ס�ODA��
�ʿɵ� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
��ã�MP��= ![]() ��
��
�֡�MN=��M��������= ![]() ��
��
��P��N= ![]() ��
�� ![]() =15��
=15��
���ɵô�ʱ��P�������Ϊ��5����15����
���Ͽɵô��������ĵ�P����P������Ϊ��5��0����5����15����
����������1����������ɵó���D��������Ϊ3������ֱ�߽���ʽ�ɵó���D�ĺ����꣬�Ӷ�����D�͵�A���������ɵó������ߵĽ���ʽ����2���ֱ����OA��OD��AD�ij��ȣ��̶����ݹ��ɶ������涨�����жϳ���OAD��ֱ�������Σ���3������ͼ�οɵõ���P�͵�N�غ�ʱ�������OPM�ס�ODA���ڹ���O��OD�Ĵ��߽��Գ����ڵ�P�䣬��ʱҲ�������P��OM�ס�ODA���������Ƶ����ʷֱ�ó���P�����꼴�ɣ�
�����㾫�������ö��κ�����ͼ��Ͷ��κ��������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ACB�У���ACB=90�㣬��ABC��ƽ����BE����BAC�����ƽ����AD�ཻ�ڵ�P���ֱ�AC��BC���ӳ�����E��D����P��PF��AD��AC���ӳ����ڵ�H����BC���ӳ����ڵ�F������AF��DH�ڵ�G�������н��ۣ��١�APB=45�㣻��PF=PA����BD��AH=AB����DG=AP+GH��������ȷ���ǣ�������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijʮ��·�ڵ������������ܼ���ֱ�У�Ҳ��������ת������ת�������ֿ����Դ�С��ͬ���������������������ʮ��·�ڣ�
��1�����á�����ͼ�����б������оٳ�������������ʻ�������п��ܵĽ����
��2��������������������ת�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B�������60km���ס������˴����س���������У����ȳ�����ͼ��![]() ��ʾ������A�صľ���s��km����ʱ��t��h���Ĺ�ϵ������ͼ�����������⣺
��ʾ������A�صľ���s��km����ʱ��t��h���Ĺ�ϵ������ͼ�����������⣺
��1����ʾ����A�صľ�����ʱ���ϵ��ͼ���� ����![]() ��
��![]() ����
����
��2�����ٶ��� km/h���ҵ��ٶ��� km/h��
��3���׳�������Сʱ����ǡ�����5km��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y1=kx+b��ͼ���뷴��������y2= ![]() ��x��0����ͼ����A��1��6����B��a��2�����㣮
��x��0����ͼ����A��1��6����B��a��2�����㣮
��1����һ�κ����뷴���������Ľ���ʽ��
��2��ֱ��д��y1��y2ʱx��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=1���Ҿ����㣨��1��0������������ͼ��д�����ĸ����ۣ�
������㣨�� ![]() ��y1���ͣ�2��y2�������������ϣ���ôy1��y2��
��y1���ͣ�2��y2�������������ϣ���ôy1��y2��
��b2��4ac��0��
��m��am+b����a+b��m��1��ʵ������
�� ![]() =��3��
=��3��
������д���ĸ������У���ȷ���У� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90�㣬AC=BC��DΪ��BC�ϵ�һ�㣬����AD������C��AD�Ĵ��ߣ�������B���ACƽ�е�ֱ���ڵ�E��CE����AB�ڵ�F.
��1�����EBF�Ķ�����
��2����֤����ACD�ա�CBE;
��3����ADƽ�֡�BAC���ж���BEF����״����˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D�ǵȱ�������ABC��һ�㣬���߶�AD�Ƶ�A˳ʱ����ת60�㣬�õ��߶�AE������CD��BE��
��1����֤����AEB=��ADC��
��2������DE������ADC=105�㣬����BED�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪�ȱߡ�OAB�Ķ���A�ڷ���������y= ![]() ��x��0��ͼ���ϣ����ȱߡ�OAB�Ķ���B����������ʱ����ȱߡ�OAB����A������͡�OAB�������
��x��0��ͼ���ϣ����ȱߡ�OAB�Ķ���B����������ʱ����ȱߡ�OAB����A������͡�OAB������� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com