
【题目】如图所示:抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过点(﹣1,0),康康依据图象写出了四个结论:
①如果点(﹣ ![]() ,y1)和(2,y2)都在抛物线上,那么y1<y2;
,y1)和(2,y2)都在抛物线上,那么y1<y2;
②b2﹣4ac>0;
③m(am+b)<a+b(m≠1的实数);
④ ![]() =﹣3.
=﹣3.
康康所写的四个结论中,正确的有( )
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】解:∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,
∴x=0与x=2时的函数值相等,由图象可知,x=0的函数值大于x=﹣ ![]() 时的函数值.
时的函数值.
∴点(﹣ ![]() ,y1)和(2,y2)都在抛物线上,则y1<y2(故①正确).
,y1)和(2,y2)都在抛物线上,则y1<y2(故①正确).
∵x=0时,函数图象与x轴两个交点,
∴ax2+bx+c=0时,b2﹣4ac>0(故②正确).
∵由图象可知,x=1时,y=ax2+bx+c取得最大值,
∴当m≠1时,am2+bm+c<a+b+c.
即m(am+b)<a+b(m≠1的实数)(故③正确).
∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过(﹣1,0)点,
∴当y=0时,x的值为﹣1或3.
∴ax2+bx+c=0时的两根之积为: ![]() ,x1x2=(﹣1)×3=﹣3.
,x1x2=(﹣1)×3=﹣3.
∴ ![]() =﹣3(故④正确).
=﹣3(故④正确).
故选D
【考点精析】根据题目的已知条件,利用二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE,动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为__________秒时.△ABP和△DCE全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动,如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.
活动中测得的数据如下:
①小明的身高DC=1.5m
②小明的影长CE=1.7cm
③小明的脚到旗杆底部的距离BC=9cm
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
请选择你需要的数据,求出旗杆的高度.(计算结果保留到0.1,参考数据 ![]() ≈1.414.
≈1.414. ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(10,0)、C(0,3),直线 ![]() 与BC相交于点D,抛物线y=ax2+bx经过A、D两点.
与BC相交于点D,抛物线y=ax2+bx经过A、D两点.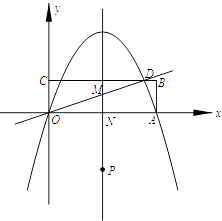
(1)求抛物线的解析式;
(2)连接AD,试判断△OAD的形状,并说明理由.
(3)若点P是抛物线的对称轴上的一个动点,对称轴与OD、x轴分别交于点M、N,问:是否存在点P,使得以点P、O、M为顶点的三角形与△OAD相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在正方形ABCD的边CD上,把△ADE绕点A顺时针旋转90°至△ABF位置,如果AB= ![]() ,∠EAD=30°,那么点E与点F之间的距离等于 .
,∠EAD=30°,那么点E与点F之间的距离等于 . 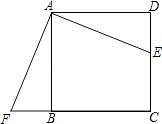
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y= ![]() ,在下列结论中,不正确的是( )
,在下列结论中,不正确的是( )
A.图象必经过点(1,2)
B.y随x的增大而减少
C.图象在第一、三象限
D.若x>1,则y<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.
(1)求运动时间t的取值范围;
(2)t为何值时,△POQ的面积最大?最大值是多少?
(3)t为何值时,以点P、0、Q为顶点的三角形与Rt△AOB相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com